Đề thi chính thức THPTQG – Môn Toán học 2023 là một trong những đề thi quan trọng thuộc Bộ Đề thi đại học môn Toán THPT, nằm trong chuyên mục Tổng hợp đề thi chính thức môn Toán học THPT QG. Đây là đề thi chính thức được Bộ Giáo dục và Đào tạo ban hành trong kỳ thi tốt nghiệp THPT năm 2023 – một kỳ thi đánh dấu sự trở lại của chương trình học đầy đủ sau giai đoạn ảnh hưởng bởi dịch bệnh.
Trong Đề thi chính thức THPTQG – Môn Toán học 2023, cấu trúc đề vẫn gồm 50 câu hỏi trắc nghiệm khách quan, trải đều kiến thức lớp 12 và có bổ sung một số nội dung lớp 11 nhằm đảm bảo tính phân hóa. Các chuyên đề trọng tâm bao gồm: khảo sát hàm số, mũ – logarit, tích phân – ứng dụng, số phức, hình học không gian cổ điển, và tổ hợp – xác suất. Đề thi có mức độ khó vừa phải, nhưng vẫn đảm bảo có các câu vận dụng cao để phân loại thí sinh khi xét tuyển đại học.
Các trọng tâm cần lưu ý trong đề thi là: nắm chắc lý thuyết cơ bản, thành thạo kỹ năng giải nhanh bằng máy tính, khả năng phân tích dữ liệu và nhận diện dạng toán. Đặc biệt, một số câu hỏi thực tế gắn với ứng dụng đời sống tiếp tục xuất hiện, đúng với định hướng đổi mới trong ra đề của Bộ.
Hãy cùng Dethitracnghiem.vn tìm hiểu chi tiết đề thi này và bắt đầu luyện đề ngay để chuẩn bị thật tốt cho kỳ thi sắp tới nhé!
Đề thi chính thức THPTQG – Môn Toán học 2023



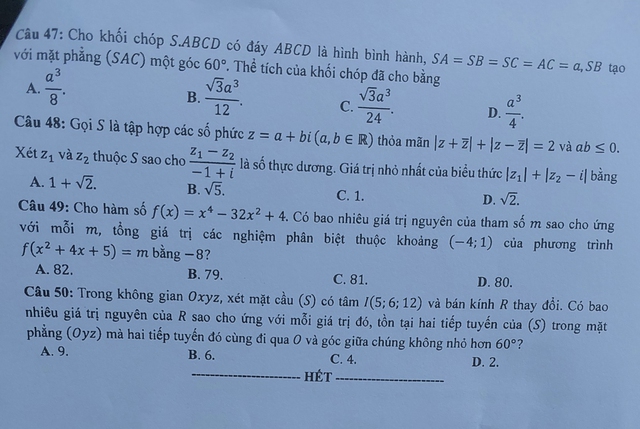
Câu 1. Trong không gian \(Oxyz\), phương trình đường thẳng \(d\) đi qua điểm \(M(-3; -1; 2)\) và có một vectơ chỉ phương \(\vec{u} = (4; 3; -2)\) là
A. \(\dfrac{x – 4}{3} = \dfrac{y – 1}{2} = \dfrac{z – 2}{4}\)
B. \(\dfrac{x + 3}{4} = \dfrac{y + 1}{3} = \dfrac{z – 2}{-2}\)
C. \(\dfrac{x + 3}{-2} = \dfrac{y + 1}{-1} = \dfrac{z – 2}{4}\)
\(\mathbf{D. \ \dfrac{x + 3}{4} = \dfrac{y + 1}{3} = \dfrac{z – 2}{-2}}\)
Câu 2. Trong không gian \(Oxyz\), mặt phẳng \((P): \dfrac{x}{5} + \dfrac{y}{2} + \dfrac{z}{1} = 1\) cắt trục \(Oy\) tại điểm có tọa độ là
A. \((0; 5; 0)\)
B. \((0; -1; 0)\)
C. \((0; 3; 0)\)
\(\mathbf{D. \ (0; 2; 0)}\)
Câu 3. Cho hình trụ có bán kính đáy bằng \(a\) và chiều cao bằng \(3a\). Diện tích xung quanh của hình trụ đã cho bằng
A. \(7\pi a^2\)
B. \(8\pi a^2\)
C. \(14\pi a^2\)
\(\mathbf{D. \ 6\pi a^2}\)
Câu 4. Cho hàm số \(y = f(x)\) có đạo hàm \(f'(x) = (x + 2)(x – 1), \ \forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là
A. \(3\)
B. \(1\)
\(\mathbf{C. \ 2}\)
D. \(0\)
Câu 5. Có bao nhiêu số tự nhiên gồm ba chữ số đôi một khác nhau mà các chữ số được lấy từ tập hợp \(\{1, 2, 3, 4, 5, 6\}\)?
A. \(216\)
B. \(20\)
C. \(18\)
\(\mathbf{D. \ 120}\)
Câu 6. Số giao điểm của đồ thị hàm số \(y = x^2 + 2x\) và trục hoành là
A. \(3\)
B. \(1\)
C. \(0\)
\(\mathbf{D. \ 2}\)
Câu 7. Cho hàm số \(y = ax^3 + bx^2 + cx + d \ (a, b, c, d \in \mathbb{R})\) có đồ thị là đường cong trong hình bên. Điểm cực tiểu của hàm số đã cho là
A. \(x = 2\)
B. \(x = -2\)
\(\mathbf{C. \ x = 1}\)
D. \(x = -1\)
Câu 8. Đạo hàm của hàm số \(y = \log_3 (x + 1)\) là
A. \(y’ = \dfrac{1}{x + 1}\)
\(\mathbf{B. \ y’ = \dfrac{1}{(x + 1)\ln 3}}\)
C. \(y’ = \dfrac{1}{\ln 3}\)
D. \(y’ = \dfrac{x + 1}{\ln 3}\)
Câu 9. Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\). Biết hàm số \(F(x)\) là một nguyên hàm của \(f(x)\) trên \(\mathbb{R}\) và \(F(1) = 3, F(3) = 6\). Tích phân \(\int_1^3 f(x)\,dx\) bằng
A. \(2\)
B. \(1\)
\(\mathbf{C. \ 3}\)
D. \(5\)
Câu 10. Diện tích đáy của khối lăng trụ có thể tích \(V\) và chiều cao \(h\) bằng
A. \(\dfrac{V}{3h}\)
B. \(\dfrac{V}{h}\)
\(\mathbf{C. \ \dfrac{V}{h}}\)
D. \(Vh\)
Câu 11. Cho cấp số nhân \((u_n)\) với \(u_1 = 2\) và \(u_2 = 8\). Công bội của cấp số nhân đã cho bằng
A. \(\dfrac{1}{4}\)
B. \(-6\)
C. \(6\)
\(\mathbf{D. \ 4}\)
Câu 12. Với \(a\) là số thực dương tùy ý, \(\log_7 (7a)\) bằng
A. \(1 – \log_7 a\)
B. \(1 + a\)
\(\mathbf{C. \ 1 + \log_7 a}\)
D. \(a\)
Câu 13. Khẳng định nào dưới đây đúng?
A. \(\int x^5\,dx = 5x^4 + C\)
B. \(\int x^5\,dx = \dfrac{x^5}{\ln 5} + C\)
\(\mathbf{C. \ \int x^5\,dx = \dfrac{1}{6}x^6 + C}\)
D. \(\int x^5\,dx = x^6 + C\)
Câu 14. Nếu \(\int_1^2 f(x)\,dx = 6\) thì \(\int_1^2 2f(x)\,dx\) bằng
A. \(4\)
\(\mathbf{B. \ 12}\)
C. \(3\)
D. \(8\)
Câu 15. Cho hình nón có bán kính đáy bằng \(a\) và chiều cao bằng \(\sqrt{3}a\). Độ dài đường sinh của hình nón đã cho bằng
A. \(\sqrt{2}a\)
B. \(4a\)
C. \(2a\)
\(\mathbf{D. \ \sqrt{10}a}\)
Câu 16. Trên mặt phẳng tọa độ, điểm \(M(-2; 2)\) là điểm biểu diễn của số phức nào dưới đây?
\(\mathbf{A. \ -2 + 2i}\)
B. \(2 – 2i\)
C. \(2 + 2i\)
D. \(-2i\)
Câu 17. Cho khối chóp có diện tích đáy \(B = 9a^2\) và chiều cao \(h = 2a\). Thể tích của khối chóp đã cho bằng
A. \(3a^3\)
B. \(18a^3\)
C. \(6a^3\)
\(\mathbf{D. \ 6a^3}\)
Câu 18. Tập nghiệm của bất phương trình \(2^x \ge 8\) là
A. \((3; +\infty)\)
B. \([-3; +\infty)\)
\(\mathbf{C. \ [3; +\infty)}\)
D. \((-\infty; 3]\)
Câu 19. Với \(a\) là số thực dương tùy ý, biểu thức \(a^3 \cdot a^2\) bằng
A. \(a^5\)
B. \(a^2\)
C. \(a^3\)
\(\mathbf{D. \ a^5}\)
Câu 20. Số phức nào dưới đây là số thuần ảo?
A. \(2i\)
B. \(2 + i\)
C. \(1 + i\)
\(\mathbf{D. \ -i}\)
Câu 21. Trong không gian \(Oxyz\), hình chiếu vuông góc của điểm \(M(-2; 3; 1)\) trên trục \(Ox\) có tọa độ là
A. \((0; 0; 1)\)
\(\mathbf{B. \ (-2; 0; 0)}\)
C. \((0; 3; 0)\)
D. \((0; 3; 1)\)
Câu 22. Trong không gian \(Oxyz\), cho mặt cầu \((S)\) có tâm \(I(1; 1; 2)\) và bán kính \(R = \sqrt{2}\). Phương trình của \((S)\) là
\(\mathbf{A. \ (x – 1)^2 + (y – 1)^2 + (z – 2)^2 = 2}\)
B. \((x + 1)^2 + (y + 1)^2 + (z – 2)^2 = 2\)
C. \((x – 1)^2 + (y + 2)^2 + (z – 1)^2 = 2\)
D. \((x – 1)^2 + (y – 1)^2 + (z + 2)^2 = 2\)
Câu 23. Cho hàm số \(y = f(x)\) có đạo hàm \(f'(x) = 3x^3, \ \forall x \in \mathbb{R}\). Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. \((-\infty; 0)\)
\(\mathbf{B. \ (0; +\infty)}\)
C. \((-\infty; +\infty)\)
D. \((0; 1)\)
Câu 24. Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho có phương trình là
A. \(x = 1\)
\(\mathbf{B. \ x = -3}\)
C. \(x = 3\)
D. \(x = -1\)
Câu 25. Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho có phương trình là
A. \(x = 1\)
B. \(x = 3\)
\(\mathbf{C. \ x = -1}\)
D. \(x = -2\)
Câu 26. Cho hàm số \(f(x) = 1 + 2\cos 2x\). Khẳng định nào dưới đây đúng?
\(\mathbf{A. \ \int f(x)\,dx = x + 2\sin 2x + C}\)
B. \(\int f(x)\,dx = x – \sin 2x + C\)
C. \(\int f(x)\,dx = x – 2\sin 2x + C\)
D. \(\int f(x)\,dx = x + \sin 2x + C\)
Câu 27. Hàm số nào dưới đây có đồ thị hình cong trong hình bên?
A. \(y = x^3 – 3x^2\)
\(\mathbf{B. \ y = x^3 + 3x^2 + 1}\)
C. \(y = x^4 – 2x^2 + 1\)
D. \(y = x^4 – 2x^2 + 1\)
Câu 28. Tập nghiệm của bất phương trình \(\log (3x) > \log 5\) là
A. \(\left(\dfrac{3}{5}; +\infty\right)\)
\(\mathbf{B. \ \left( \dfrac{5}{3}; +\infty \right)}\)
C. \(\left(0; 5\right)\)
D. \(\left(3; 5\right)\)
Câu 29. Trong không gian \(Oxyz\), cho hai điểm \(A(1; 2; 3)\) và \(B(-1; 0; 5)\). Phương trình của mặt cầu đi qua điểm \(A\) và bán kính \(R = 2\) là
A. \((x + 2)^2 + (y – 1)^2 + (z – 4)^2 = 3\)
B. \((x – 1)^2 + (y – 2)^2 + (z – 4)^2 = 3\)
C. \((x – 1)^2 + (y – 2)^2 + (z – 2)^2 = 3\)
\(\mathbf{D. \ (x – 1)^2 + (y + 1)^2 + (z + 2)^2 = 4}\)
Câu 30. Dương gấp khúc \(ABC\) trong hình bên là đồ thị của hàm số \(y = f(x)\) trên đoạn \([1; 4]\). Tích phân \(\int_1^4 f(x)\,dx\) bằng
A. \(4\)
B. \(7\)
\(\mathbf{C. \ 3}\)
D. \(6\)
Câu 31. Cho hàm số bậc bốn \(y = f(x)\) có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho \(f(x) = m\) có đúng 4 nghiệm thực phân biệt?
A. \(8\)
B. \(17\)
\(\mathbf{C. \ 16}\)
D. \(4\)
Câu 32. Tập xác định của hàm số \(f(x) = \log (30 – x^2)\) chứa bao nhiêu số nguyên?
A. \(11\)
B. \(6\)
C. \(10\)
\(\mathbf{D. \ 5}\)
Câu 33. Hàm số \(y = x^4 – 2x^2\) nghịch biến trên khoảng nào dưới đây?
A. \((1; +\infty)\)
B. \((- \infty; 1)\)
\(\mathbf{C. \ (-\infty; 0)}\)
D. \((-1; 0)\)
Câu 34. Cho hình hộp chữ nhật \(ABCD.A’B’C’D’\) có \(AB = 1\), \(BC = 2\), \(AA’ = 2\), góc giữa hai mặt phẳng \((A’BD)\) và \((ABC)\) bằng \(60^\circ\). Khoảng cách giữa hai đường thẳng \(AB’\) và \(BC’\) bằng
A. \(\sqrt{2}\)
B. \(3\sqrt{3}\)
\(\mathbf{C. \ \sqrt{6}}\)
D. \(4\)
Câu 35. Cho hình chóp đều \(SABCD\) có đáy là tứ giác cạnh bằng \(a\). Góc giữa hai đường thẳng \(SB\) và \(CD\) bằng
A. \(30^\circ\)
B. \(45^\circ\)
\(\mathbf{C. \ 90^\circ}\)
D. \(60^\circ\)
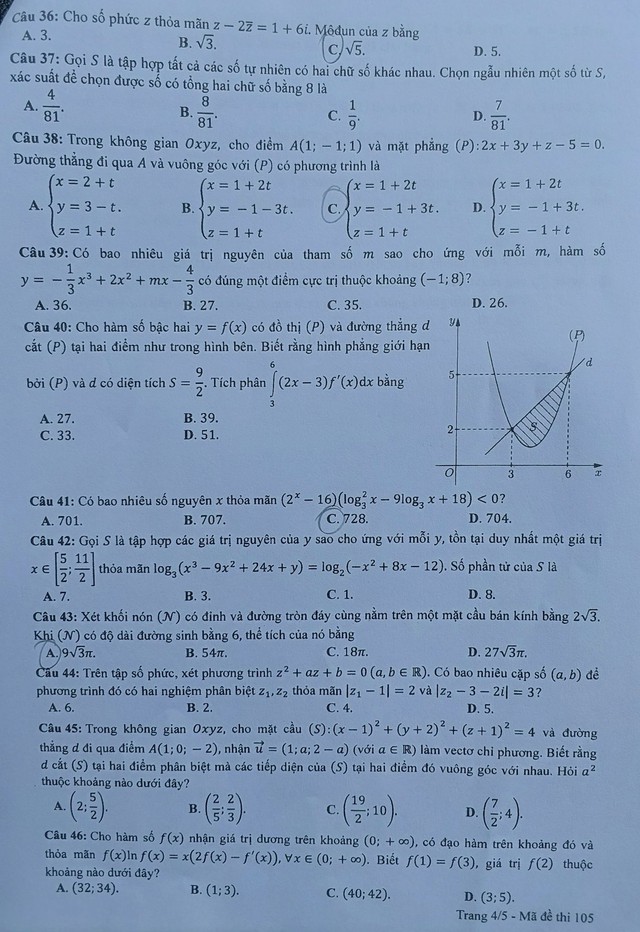
Câu 36. Cho số phức \(z\) thỏa mãn \(z – 2z = 1 + 6i\). Môđun của \(z\) bằng
A. \(3\)
B. \(\sqrt{3}\)
C. \(\sqrt{5}\)
\(\mathbf{D. \ 5}\)
Câu 37. Gọi \(S\) là tập hợp tất cả các số tự nhiên có hai chữ số khác nhau. Chọn ngẫu nhiên một số từ \(S\), xác suất để chọn được số có tổng hai chữ số bằng 8 là
A. \(\dfrac{4}{81}\)
B. \(\dfrac{7}{81}\)
C. \(\dfrac{1}{9}\)
\(\mathbf{D. \ \dfrac{7}{81}}\)
Câu 38. Trong không gian \(Oxyz\), cho điểm \(A(1; -1; 1)\) và mặt phẳng \((P): 2x + 3y + z = 5 = 0\). Đường thẳng đi qua \(A\) và vuông góc với \((P)\) có phương trình là
A. \(\begin{cases} x = 1 + 2t \\ y = -1 + t \\ z = 1 + t \end{cases}\)
B. \(\begin{cases} x = 1 + 2t \\ y = -1 + 3t \\ z = 1 + t \end{cases}\)
C. \(\begin{cases} x = 1 + t \\ y = -1 + 2t \\ z = 1 + 3t \end{cases}\)
\(\mathbf{D. \ \begin{cases} x = 1 + 2t \\ y = -1 + t \\ z = 1 + t \end{cases}}\)
Câu 39. Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho phương trình \(y = x^3 + 3x^2 + mx + 4\) có đúng một điểm cực trị thuộc khoảng \((-1; 8)\)?
A. \(36\)
B. \(27\)
C. \(35\)
\(\mathbf{D. \ 26}\)
Câu 40. Cho hàm số bậc hai \(y = f(x)\) có đồ thị \(y = f(x)\) và \(f(x)\) là đường thẳng cắt tại điểm có diện tích bằng
A. \(10\)
\(\mathbf{B. \ 12}\)
C. \(3\)
D. \(8\)
Câu 41. Có bao nhiêu số nguyên \(x\) thỏa mãn \((2x – 16)(\log_3 x – 9log_3 x + 18) < 0\)?
A. \(701\)
B. \(707\)
C. \(728\)
\(\mathbf{D. \ 704}\)
Câu 42. Gọi \(S\) là tập hợp các giá trị nguyên của \(y\) sao cho mọi giá trị \(x = \dfrac{5}{2}\) thỏa mãn \(\log(x^3 – 9x^2 + 24x + y) = \log(x^2 – 8x – 12)\). Số phần tử của \(S\) là
A. \(7\)
B. \(3\)
C. \(1\)
\(\mathbf{D. \ 8}\)
Câu 43. Kết khối nón \(N(y)\) có định và đường tròn đáy cùng nằm trên mặt cầu bán kính bằng \(2\sqrt{3}\). Diện tích xung quanh của khối nón là \(\sqrt{3}\). Diện tích của hình cầu là
A. \(5\sqrt{3}\)
B. \(54\pi\)
C. \(18\pi\)
\(\mathbf{D. \ 27\pi}\)
Câu 44. Trên tập số phức, xét phương trình \(z^2 + az + b = 0\) với \(a, b \in \mathbb{C}\). Cần bao nhiêu tập hợp các số nghiệm phức sao cho phương trình có nghiệm phân biệt \(z_1, z_2\) là số phức với mô đun \(|z_1| = 1\)?
A. \(6\)
B. \(9\)
C. \(4\)
\(\mathbf{D. \ 3}\)
Câu 45. Trong không gian \(Oxyz\), cho mặt cầu \((S): (x – 1)^2 + (y + 2)^2 + (z + 1)^2 = 4\) và đường thẳng \(d\) đi qua điểm \(A(1; 0; -2)\), nhận \(\vec{u} = (1; a; 2 – a)\) (với \(a \in \mathbb{R}\)) làm vectơ chỉ phương. Biết rằng \(d\) cắt \(S\) tại điểm phân biệt mà các tiếp tuyến của \((S)\) tại điểm đó vuông góc với nhau. Hỏi \(a^2\) thuộc khoảng nào dưới đây?
A. \(\left(\dfrac{5}{2}; \dfrac{7}{2}\right)\)
\(\mathbf{B. \ \left(\dfrac{2}{3}; \dfrac{5}{3}\right)}\)
C. \(\left(\dfrac{19}{2}; \dfrac{10}{2}\right)\)
D. \(\left(7; \dfrac{7}{2}\right)\)
Câu 46. Cho hàm số \(f(x)\) nhận giá trị dương trên khoảng \((0; + \infty)\), có đạo hàm trên khoảng đó và thỏa mãn \(f(x) \ln f(x) = x \left(2f(x) – f'(x)\right)\), với \(x \in (0; + \infty)\). Biết \(f(1) = 3\), giá trị \(f(2)\) thuộc khoảng nào dưới đây?
A. \((32; 34)\)
B. \((1; 3)\)
\(\mathbf{C. \ (40; 42)}\)
D. \((3; 5)\)
Câu 47. Cho khối chóp \(SABCD\) có đáy \(ABCD\) là hình bình hành, \(SA = SB = SC = AC = a\), \(SB\) tạo với mặt phẳng \((SAC)\) một góc \(60^\circ\). Thể tích của khối chóp đã cho bằng
A. \(\dfrac{a^3}{3}\)
B. \(\dfrac{\sqrt{3}a^3}{12}\)
\(\mathbf{C. \ \dfrac{\sqrt{3}a^3}{24}}\)
D. \(\dfrac{a^3}{4}\)
Câu 48. Gọi \(S\) là tập hợp các số phức \(z = a + bi\) \((a, b \in \mathbb{R})\) thỏa mãn \(\left|z – 1\right| = \left|z + 1\right|\) và \(\left|z\right| \leq 0\).
Xét \(z_1 \neq z_2\) thuộc \(S\) sao cho \(z_1 – z_2\) là số thuần dương. Giá trị nhỏ nhất của biểu thức \(\left|z_1 – z_2\right|\) là
A. \(1\)
B. \(\sqrt{2}\)
\(\mathbf{C. \ 5}\)
D. \(6\)
Câu 49. Cho hàm số \(f(x) = x^4 – 32x^2 + 4\). Có bao nhiêu giá trị nguyên của \(m\) sao cho ứng với mỗi \(m\), tổng giá trị các nghiệm phân biệt thuộc khoảng \((-4; 1)\) của phương trình \(f(x) = m\) bằng \(8\)?
A. \(82\)
B. \(79\)
\(\mathbf{C. \ 81}\)
D. \(80\)
Câu 50. Trong không gian \(Oxyz\), xét mặt cầu \((S)\) có tâm \(I(5; 6; 12)\) và bán kính \(R\) thay đổi. Có bao nhiêu giá trị nguyên của \(R\) sao cho ứng với mỗi giá trị đó, tồn tại hai tiếp tuyến của mặt phẳng \((Oyz)\) mà hai tiếp tuyến đó cùng đi qua \(O\) và góc giữa chúng không nhỏ hơn \(60^\circ\)?
A. \(9\)
B. \(6\)
C. \(4\)
\(\mathbf{D. \ 2}\)
Mục đích tổ chức thi tốt nghiệp THPT 2023 là gì?
Căn cứ theo Mục 1 Phương án Tổ chức kỳ thi và xét công nhận tốt nghiệp trung học phổ thông từ năm 2023 ban hành kèm theo Quyết định 4068/QĐ-BGDĐT 2023, mục đích tổ chức thi tốt nghiệp THPT 2023 để:
– Đánh giá đúng kết quả học tập của người học theo mục tiêu và chuẩn cần đạt theo yêu cầu của Chương trình giáo dục phổ thông (GDPT) 2020
– Lấy kết quả thi để xét công nhận tốt nghiệp trung học phổ thông (THPT) và làm một trong các cơ sở để đánh giá chất lượng dạy, học của các cơ sở GDPT và công tác chỉ đạo của các cơ quan quản lý giáo dục.
– Cung cấp dữ liệu đủ độ tin cậy cho các cơ sở giáo dục đại học, giáo dục nghề nghiệp sử dụng trong tuyển sinh theo tinh thần tự chủ.
Thí sinh thi tốt nghiệp THPT 2023 có bắt buộc thi môn Toán học không?
Căn cứ theo Mục 5 Phương án Tổ chức kỳ thi và xét công nhận tốt nghiệp trung học phổ thông từ năm 2023 ban hành kèm theo Quyết định 4068/QĐ-BGDĐT 2023 quy định như sau:
Thí sinh thi bắt buộc môn Ngữ văn, môn Toán và 02 môn thí sinh tự chọn trong số các môn còn lại được học ở lớp 12 (Ngoại ngữ, Lịch sử, Vật lí, Hóa học, Sinh học, Địa lí, Giáo dục kinh tế và pháp luật, Tin học, Công nghệ).
Đồng thời, căn cứ theo Điều 3 Quy chế thi tốt nghiệp trung học phổ thông ban hành kèm theo Thông tư 24/2024/TT-BGDĐT quy định như sau:
Môn thi
Tổ chức kỳ thi gồm 03 buổi thi: 01 buổi thi môn Ngữ văn, 01 buổi thi môn Toán và 01 buổi thi của bài thi tự chọn gồm 02 môn thi trong số các môn: Vật lí, Hóa học, Sinh học, Lịch sử, Địa lí, Giáo dục kinh tế và pháp luật, Tin học, Công nghệ định hướng Công nghiệp (gọi tắt là Công nghệ Công nghiệp), Công nghệ định hướng Nông nghiệp (gọi tắt là Công nghệ Nông nghiệp), Ngoại ngữ (Tiếng Anh, Tiếng Nga, Tiếng Pháp, Tiếng Trung Quốc, Tiếng Đức, Tiếng Nhật và Tiếng Hàn).
Theo quy định này, các môn thi tốt nghiệp THPT 2023 bao gồm:
– Thi 02 môn bắt buộc: Toán và Ngữ văn.
– Thi 02 môn tự chọn trong số các môn sau: Vật lí, Hóa học, Sinh học, Lịch sử, Địa lí, Giáo dục kinh tế và pháp luật, Tin học, Công nghệ định hướng Công nghiệp, Công nghệ định hướng Nông nghiệp, Ngoại ngữ.
Như vậy, kỳ thi tốt nghiệp THPT 2023 bắt buộc thí sinh phải thi môn Toán học.




