Đề tham khảo tuyển sinh lớp 10 môn Toán (lớp thường) năm 2025 trường chuyên ĐHSP Hà Nội là một trong những đề tham khảo môn Toán không chuyên tuyển sinh lớp 10 trong Bộ đề thi thử tuyển sinh lớp 10 môn Toán. Đây là đề thi được Trường THPT chuyên ĐHSP Hà Nội thiết kế dành cho các thí sinh thi vào lớp 10 hệ không chuyên, với cấu trúc bám sát chương trình THCS và mức độ tương đương đề thi tuyển sinh công lập.
Đề thi chuyển cấp lớp 10 bao gồm các chuyên đề trọng tâm như: giải phương trình – hệ phương trình, biến đổi biểu thức, hàm số và đồ thị, bài toán thực tế, và các bài toán hình học phẳng quen thuộc như chứng minh, tính toán diện tích hoặc độ dài. Đề thi được thiết kế với độ khó vừa phải, có phân hóa, nhằm kiểm tra toàn diện kiến thức nền tảng và kỹ năng giải toán cơ bản đến nâng cao của học sinh.
Việc luyện tập với Đề tham khảo tuyển sinh lớp 10 môn Toán (chung) năm 2025 trường chuyên ĐHSP Hà Nội sẽ giúp học sinh hệ thống lại kiến thức, nâng cao khả năng tư duy logic và trình bày bài làm rõ ràng, đồng thời chuẩn bị tốt cho kỳ thi vào lớp 10 tại các trường chất lượng cao và chuyên sâu về học thuật.
Hãy cùng Dethitracnghiem.vn cùng tìm hiểu về đề thi này và tham gia làm kiểm tra ngay lập tức!
- Số trang: 3 trang
- Hình thức: trắc nghiệm + tự luận
- Thời gian làm bài: 120 phút (không kể thời gian phát đề)
Đề tham khảo tuyển sinh lớp 10 môn Toán (chung) năm 2025 trường chuyên ĐHSP Hà Nội







A. PHẦN TRẮC NGHIỆM (3,0 điểm) * Thí sinh trả lời câu hỏi bằng cách tô trên Phiếu trả lời trắc nghiệm; bài làm được quét bằng máy và chấm tự động bằng phần mềm. Trong mỗi câu, thí sinh chỉ chọn một phương án.
Câu 1. Biểu đồ ở Hình bên cho biết thu nhập bình quân đầu người/năm của Việt Nam (tính theo đô la Mỹ) ở một số năm trong giai đoạn từ năm 1986 đến năm 2020. Thu nhập bình quân đầu người năm 2019 là bao nhiêu đô la Mỹ?
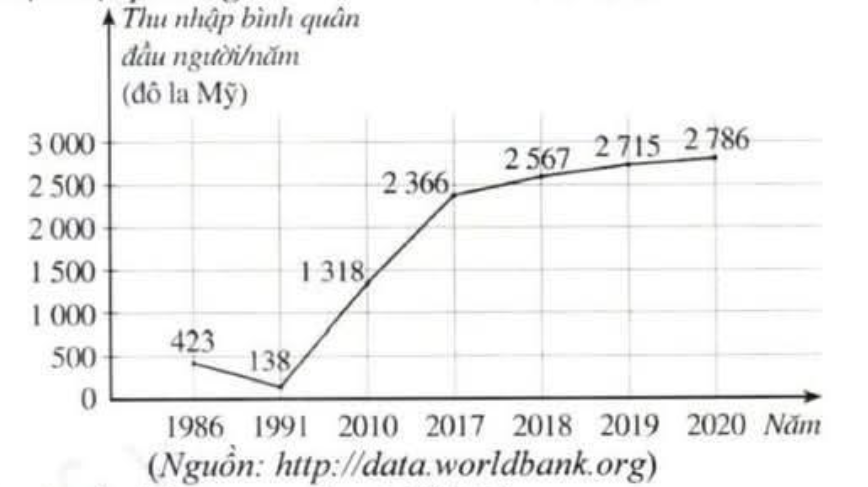
A. 2 786 đô la Mỹ.
B. 2 715 đô la Mỹ.
C. 2 567 đô la Mỹ.
D. 2366 đô la Mỹ.
Câu 2: Bảng dưới đây cho biết nhiệt độ trung bình của các tháng trong năm ở Hà Nội.
 Nhiệt độ trung bình của tháng 5 là
Nhiệt độ trung bình của tháng 5 là
A. 20,2°C
B. 23,7°C
C. 27,3°C
D. 28,8°C
Câu 3: Một hộp có 26 viên bi gồm: 5 viên bi xanh, 6 viên bi đỏ, 7 viên bi vàng và 8 viên bi tím; các viên bi có hình dạng và kích thước như nhau. Xét phép thử: “Lấy ngẫu nhiên 1 viên bi trong hộp”. Xác suất của biến cố “Viên bi được lấy ra có màu tím” bằng
A. $\frac{5}{26}$
B. $\frac{6}{26}$
C. $\frac{7}{26}$
D. $\frac{8}{26}$
Câu 4: Nếu a là số thực khác 0 thì biểu thức M = a¹⁰ : a² bằng
A. a⁸
B. a⁵
C. a¹²
D. a²⁰
Câu 5: Cho hai số thực a, b. Phát biểu nào sau đây là đúng?
A. (a – b)² = a² – 2ab – b²
B. (a – b)² = a² – b²
C. (a – b)² = a² – ab + b²
D. (a – b)² = a² – 2ab + b²
Câu 6: Căn bậc hai số học của số 4 bằng
A. -2
B. 4
C. 2
D. 16
Câu 7: Phát biểu nào sau đây là đúng?
A. Đồ thị của hàm số y = 3x² nhận trục Ox làm trục đối xứng.
B. Đồ thị của hàm số y = 3x² nhận trục Oy làm trục đối xứng.
C. Đồ thị của hàm số y = 3x² nhận đường thẳng y = x làm trục đối xứng.
D. Đồ thị của hàm số y = 3x² nhận đường thẳng y = -x làm trục đối xứng.
Câu 8: Trong mặt phẳng tọa độ Oxy, đường thẳng nào sau đây song song với đường thẳng y = -2x + 3?
A. y = -2x + 1.
B. y = 2x + 3.
C. y = -3x + 2.
D. y = 2x – 3.
Câu 9: Nếu ABCD là tứ giác nội tiếp và $\widehat{A}$ = 40° thì
A. $\widehat{C}$ = 40°.
B. $\widehat{C}$ = 20°.
C. $\widehat{C}$ = 140°.
D. $\widehat{C}$ = 80°.
Câu 10: Một cái bánh ít lá gai có dạng hình chóp tứ giác đều với cạnh đáy bằng 4 cm và chiều cao bằng 3,6 cm. Thể tích của cái bánh này bằng bao nhiêu cm³?
A. 13, 6 cm³.
B. 19, 2 cm³.
C. 6, 4 cm³.
D. 7, 6 cm³.
Câu 11: Một hộp đựng thực phẩm có dạng hình lập phương có thể tích bằng 64 dm³.
Diện tích xung quanh của hộp đựng thực phẩm đó bằng bao nhiêu dm²?
A. 96 dm².
B. 64 dm².
C. 16 dm².
D. 32 dm².
Câu 12: Một mảnh vườn có dạng hình thang vuông được minh họa như hình bên. Biết $\widehat{A}$ = $\widehat{B}$ = 90°, AB = 12m, BC = 20m và AD = 11m. Độ dài của CD bằng bao nhiêu mét?
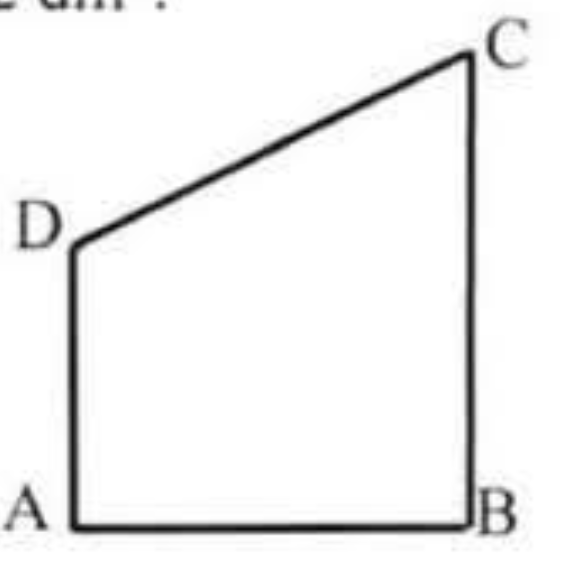
A. $\sqrt{240}$m.
B. $\sqrt{220}$m.
C. $\frac{43}{3}$m.
D. 15 m.
B. PHẦN TỰ LUẬN (7,0 điểm)
* Thí sinh làm bài trên tờ giấy thi.
Câu 13 (1,0 điểm). Một nhà may đo chiều cao của 160 học sinh nữ lớp 9 (đơn vị: cm). Nhà may đã thu thập số liệu và ghép thành 5 nhóm: [160;162), [162;164), [164;166), [166;168), [168;170) và lập bảng tần số ghép nhóm sau đây:

(trong đó nhóm [a;b) gồm các số đo chiều cao lớn hơn hoặc bằng a và nhỏ hơn b)
a) Tính tần số và tần số tương đối của nhóm [166;168).
b) Chọn ngẫu nhiên một học sinh nữ lớp 9 trong số 160 học sinh nữ được đo chiều cao. Xác suất chọn được bạn có chiều cao thuộc nhóm [168;170) là bao nhiêu?
Câu 14 (2,5 điểm)
a) (1,0 điểm) Nhân dịp Ngày Quốc tế lao động 1/5, một siêu thị điện máy đã giảm giá nhiều mặt hàng để kích cầu mua sắm. Tổng số tiền theo giá niêm yết của một chiếc điều hòa nhiệt độ và một chiếc ti vi là 25 triệu đồng. Tuy nhiên, trong dịp này giá một chiếc điều hòa nhiệt độ giảm 35% so với giá niêm yết và giá một chiếc ti vi giảm 30% so với giá niêm yết. Vì thế, cô Hoa đã mua một chiếc điều hòa nhiệt độ và một chiếc ti vi với tổng số tiền là 16 750 000 đồng. Hỏi giá niêm yết mỗi mặt hàng trên là bao nhiêu?
b) (1,0 điểm) Cho phương trình x² + 2mx – m² – 2 = 0 với m là tham số khác 0. Chứng minh rằng phương trình luôn có hai nghiệm x₁, x₂ trái dấu thỏa mãn x₁ > 0 > x₂ và $\frac{1}{\sqrt{x₁² + \sqrt{-x₁x₂}}}$ + $\frac{1}{\sqrt{x₂² – \sqrt{-x₁x₂}}}$ = $\frac{1}{m²}$
c) (0,5 điểm) Cho hai đa thức P(x) = x³ + x + 1 và Q(x) = x⁴ – x³ + x² + 2025. Giả sử số a là một nghiệm của đa thức P(x). Tính giá trị của biểu thức Q(a).
Câu 15 (2,5 điểm). Cho tam giác ABC cân tại A và nội tiếp đường tròn (O). Gọi M là trung điểm của cạnh BC. Lấy điểm D tùy ý nằm trên cung AC không chứa điểm B (D khác A và C). Gọi H là hình chiếu vuông góc của điểm A trên đường thẳng BD.
a) (0,5 điểm). Chứng minh rằng bốn điểm A, B, M, H cùng thuộc một đường tròn.
b) (1,0 điểm). Chứng minh MH vuông góc với AD.
c) (1,0 điểm). Cho $\widehat{BAC}$ = 40°, tính $\frac{BD – CD}{AH}$ (làm tròn kết quả đến hàng phần mười).
Câu 16 (1,0 điểm). Một cửa hàng điện tử dự định sử dụng số vốn ban đầu không vượt quá 2 tỉ 750 triệu đồng để nhập về hai loại ti vi: loại 50 inch và loại 55 inch. Giá nhập và lợi nhuận dự kiến của mỗi loại ti vi được tính trong bảng sau:

Cửa hàng ước tính rằng tổng nhu cầu tiêu thụ của thị trường sẽ không vượt quá 120 chiếc ti vi cả hai loại. Tính số lượng ti vi mỗi loại mà cửa hàng nên nhập về để lợi nhuận thu được (sau khi bán hết hàng nhập về) là lớn nhất.




