Đề thi thử đại học môn Toán 2025 – THPT Lương Ngọc Quyến – Thái Nguyên (Lần 1) là một trong những đề thi tiêu biểu thuộc chuyên mục Thi chuyển cấp môn Toán THPT. Đây là đề thi nằm trong chương Thi thử Toán THPT, được thiết kế nhằm phục vụ cho mục đích Ôn tập thi thử THPT, giúp học sinh lớp 12 nâng cao kỹ năng giải đề, làm quen với áp lực thời gian và nhận diện các dạng bài thường xuất hiện trong đề thi tốt nghiệp THPT.
Cấu trúc đề thi bám sát đề minh họa của Bộ Giáo dục và Đào tạo, bao quát đầy đủ các chuyên đề trọng tâm trong chương trình Toán lớp 12 như: hàm số và đồ thị, mũ – logarit, nguyên hàm – tích phân, hình học không gian Oxyz, số phức, xác suất – thống kê. Đặc biệt, các câu hỏi trong đề có sự phân loại rõ ràng, từ mức độ nhận biết đến vận dụng cao, phù hợp cho học sinh luyện tập và đánh giá năng lực một cách toàn diện.
Hãy cùng Dethitracnghiem.vn tìm hiểu về đề thi này và tham gia làm kiểm tra ngay lập tức!
Đề thi thử đại học môn Toán 2025 – THPT Lương Ngọc Quyến – Thái Nguyên (Lần 1)
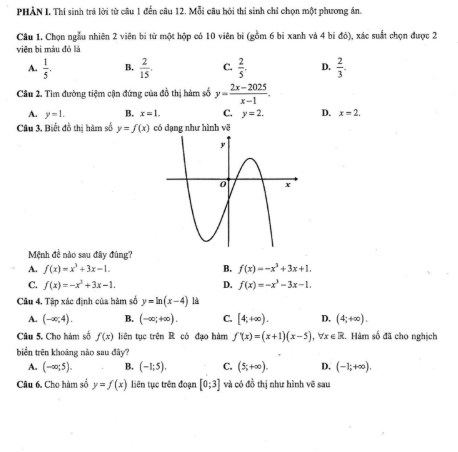



PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Chọn ngẫu nhiên 2 viên bi từ một hộp có 10 viên bi (gồm 6 bi xanh và 4 bi đỏ), xác suất được 2 viên bi màu đỏ là
A. $\frac{1}{5}$
B. $\frac{2}{15}$
C. $\frac{2}{5}$
D. $\frac{2}{3}$
Câu 2: Tìm đường tiệm cận đứng của đồ thị hàm số $y = \frac{2x-2025}{x-1}$.
A. y = 1.
B. x = 1.
C. y = 2.
D. x = 2.
Câu 3: Đồ thị hàm số y = f(x) có dạng như hình vẽ
Mệnh đề nào sau đây đúng?
A. $f(x) = x^3 + 3x – 1.$
B. $f(x) = -x^3 + 3x + 1.$
C. $f(x) = -x^3 + 3x – 1.$
D. $f(x) = x^3 – 3x – 1.$
Câu 4: Tập xác định của hàm số $y = \ln(x – 4)$ là
A. $(-∞; 4)$.
B. $(-∞; +∞)$.
C. $[4; +∞)$.
D. $(4; +∞)$.
Câu 5: Cho hàm số $f(x)$ liên tục trên R có đạo hàm $f'(x) = (x+1)(x-5), ∀x ∈ R$. Hàm số đã cho nghịch biến trên khoảng nào sau đây?
A. $(-∞; 5)$.
B. $(-1; 5)$.
C. $(5; +∞)$.
D. $(-1; +∞)$.
Câu 6: Cho hàm số $y = f(x)$ liên tục trên đoạn [0;3] và có đồ thị như hình vẽ sau
Tổng giá trị lớn nhất và nhỏ nhất của hàm số $y = f(x)$ trên đoạn [0;3] bằng
A. 5.
B. 2.
C. 1.
D. 3.
Câu 7: Giới hạn $\lim_{x \to -∞} \frac{2x-3}{1-3x}$ bằng
A. $\frac{-2}{3}$
B. $\frac{2}{3}$
C. 2.
D. 1.
Câu 8: Cho tứ diện ABCD. Mệnh đề nào dưới đây là mệnh đề đúng?
A. $\overrightarrow{BA} – \overrightarrow{DA} = \overrightarrow{DC} + \overrightarrow{CB}$.
B. $\overrightarrow{DC} + \overrightarrow{AD} = \overrightarrow{BA} – \overrightarrow{CA}$.
C. $\overrightarrow{CA} – \overrightarrow{DA} = \overrightarrow{DB} – \overrightarrow{CB}$.
D. $\overrightarrow{BD} – \overrightarrow{BA} = \overrightarrow{CD} – \overrightarrow{BC}$.
Câu 9: Cho mẫu số liệu về cân nặng của 58 học sinh như sau:
| Cân nặng (kg) | [40;50) | [50;60) | [60;70) | [70;80) |
|—|—|—|—|—|
| Số học sinh | 5 | 8 | 25 | 20 |
Trung vị mẫu số liệu là
A. $M_e = 66,4$.
B. $M_e = 60,8$.
C. $M_e = 65$.
D. $M_e = 60$.
Câu 10: Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu của $f'(x)$ như hình dưới đây
| x | -∞ | -1 | 1 | +∞ |
|—|—|—|—|—|
| f'(x) | | – | 0 | + |
Hàm số y = f(x) có bao nhiêu điểm cực trị?
A. 0.
B. 1.
C. 3.
D. 2.
Câu 11: Trong không gian Oxyz, cho hai vector $\overrightarrow{u} = (1;-2;3)$ và $\overrightarrow{v} = (5;4;-1)$. Tọa độ của vector $\overrightarrow{u} – \overrightarrow{v}$ là
A. $\overrightarrow{u} – \overrightarrow{v} = (4; 6; -4)$.
B. $\overrightarrow{u} – \overrightarrow{v} = (4; -6; 4)$.
C. $\overrightarrow{u} – \overrightarrow{v} = (-4; -6; 4)$.
D. $\overrightarrow{u} – \overrightarrow{v} = (-4; 6; -4)$.
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = a, AD = 2a. Cạnh bên SA vuông góc với đáy và SA = 3a. Thể tích khối chóp S.ABCD bằng
A. $6a^3$.
B. $\frac{3a^3}{2}$.
C. $2a^3$.
D. $3a^3$.
PHẦN II
**Câu 1.** Một bác tài xế thống kê lại số liệu quãng đường bác đã lái xe mỗi ngày trong một tháng ở bảng sau:
| Quãng đường (km) | [50; 100) | [100; 150) | [150; 200) | [200; 250) | [250; 300) |
|—|—|—|—|—|—|
| Số ngày | 5 | 10 | 9 | 4 | 2 |
a) Số trung bình của mẫu số liệu ghép nhóm là 145.
b) Khoảng biến thiên của mẫu số liệu ghép nhóm là 250 (km).
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm bằng 79,17 (kết quả làm tròn đến hàng phần trăm).
d) Độ lệch chuẩn của mẫu số liệu ghép nhóm bằng 55,68 (kết quả làm tròn đến hàng phần trăm).
**Câu 2.** Cho hàm số $f(x) = 4x – log_2(x+1)$.
a) Hàm số $f(x)$ nghịch biến trên khoảng nào $(0; +\infty)$.
b) Giá trị của hàm số $f(x)$ tại điểm $x=1$ là **$f(1) = 4$**.
c) Đạo hàm của hàm số $f(x)$ là $f'(x) = 4 – \frac{1}{(x+1)ln2}, \forall x \in (-1; +\infty)$.
d) Hàm số $f(x)$ có hai điểm cực trị.
**Câu 3.** Một cửa hàng bán vải thiều Bắc Giang với giá bán là 30000 đồng/1 kg. Giá nhập vào là 16000 đồng/1 kg. Với giá này của hàng ước chừng bán được 100kg/1 ngày. Cửa hàng dự định giảm giá bán, ước tính cứ giảm 1000 đồng/1 kg thì số vải thiều bán được sẽ tăng thêm là 10kg.
a) Lợi nhuận tối đa theo ngày của cửa hàng là 1440000 đồng.
b) Nếu giá bán là 20000 đồng/1 kg, khi đó cửa hàng bán được 250 kg/1 ngày.
c) Nếu giá bán là 25000 đồng/1 kg, khi đó lợi nhuận theo ngày của cửa hàng là 1350000 đồng.
d) Nếu giữ nguyên giá bán đầu, lợi nhuận theo ngày của cửa hàng là 1500000 đồng.
**Câu 4.** Hệ thống cáp treo gồm hai trụ lớn và một đường cáp nói thẳng giữa hai trụ đó (coi như độ cong không đáng kể), được đặt trong không gian với hệ tọa độ Oxyz. Một cabin cáp treo xuất phát từ điểm O(0;0;0) thuộc trụ thứ nhất và chuyển động thẳng đều theo đường cáp đến điểm A(896;2025;189) thuộc trụ thứ hai với tốc độ là 7,4 (m/s) (đơn vị trên mỗi trục là mét).
a) Độ dài đường cáp xấp xỉ bằng 2222 m (kết quả làm tròn đến hàng đơn vị).
b) Trên đường cáp có điểm B với hoành độ $x_B = 672$, khi đó thời gian để cabin đi từ điểm B đến điểm A xấp xỉ là 80 giây (kết quả làm tròn đến hàng đơn vị).
c) Có một khu vui chơi phía dưới cáp treo nằm trong mặt phẳng (Oxy) với điểm trung tâm có tọa độ (750;5;1497,25; 0). Biết rằng từ trong cabin cáp treo có thể ngắm nhìn toàn cảnh khu vui chơi rõ nhất tại vị trí điểm M($x_M$;$y_M$;$z_M$) cách trung tâm khu vui chơi một khoảng ngắn nhất. Khi đó, ta có $x_M + y_M + z_M$ = 2335,5 (kết quả làm tròn đến hàng phần mười).
d) Điểm chính giữa của đường cáp có tọa độ là (448; 1012,5; 94,5).
**Phần III.** Thí sinh trả lời từ câu 1 đến câu 6.
**Câu 1.** Một công ty kinh doanh dịch vụ nghỉ dưỡng nhận thấy rằng: Nếu áp dụng mức giá 4 triệu đồng/người/ngày thì mỗi tháng có 180 khách đến nghỉ và mỗi khách nghỉ 11 ngày. Nếu cứ tăng giá thêm 500 nghìn đồng/người/ngày thì hàng tháng số khách đến nghỉ sẽ giảm đi 8 người và thời gian lưu trú của mỗi người khách cũng giảm đi 4 ngày. Ngược lại, nếu cứ giảm giá 500 nghìn đồng/người/ngày thì hàng tháng số khách đến nghỉ sẽ tăng thêm 8 người và thời gian lưu trú của mỗi người khách cũng tăng thêm 4 ngày. Hỏi công ty cần áp dụng mức giá bao nhiêu triệu đồng/người/ngày để lợi nhuận hàng tháng thu được là lớn nhất, biết rằng chi phí công ty phải chi cho một ngày lưu trú của mỗi người khách là 1 triệu đồng và Sở du lịch không cho công ty thu quá 10 triệu đồng/người/ngày (kết quả làm tròn đến hàng phần trăm).
**Câu 2.** Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng 8 và thể tích bằng 18. Gọi G là trọng tâm của tam giác SCD, trên các cạnh AB,SD lần lượt lấy các điểm E,F sao cho EF song song BG. Khoảng cách giữa hai đường thẳng DG và EF bằng $\frac{m}{n}$ với m, n là số nguyên dương và $\frac{m}{n}$ là phân số tối giản. Tính giá trị của biểu thức $T = 2m – n$.
**Câu 3.** Một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông cạnh x (cm) và chiều cao h (cm). Biết tổng diện tích các bề mặt của chiếc hộp bằng 192 $cm^2$. Tìm x để chiếc hộp có thể tích lớn nhất?
**Câu 4.** Trong không gian Oxyz, cho tam giác ABC biết: A(1;-1;2), B(-2;0;3), C(0;1;-2). Gọi M (a;b;c) là điểm thuộc mặt phẳng (Oxy) sao cho biểu thức $S = MA.MB + MB.MC + 6MC.MA$ đạt giá trị nhỏ nhất. Tính giá trị $T = 16a + 16b – 2c$.
**Câu 5.** Một xí nghiệp may áo vest và quần âu để chuẩn bị cho dịp cuối năm. Biết may 1 áo vest hết 2m vải và cần 20 giờ; may 1 quần âu hết 1,5m vải và cần 5 giờ. Xí nghiệp được giao sử dụng không quá 930 m vải và số giờ công không vượt quá 6300 giờ. Theo khảo sát thị trường, số lượng quần âu bán ra không nhỏ hơn số lượng áo vest bán ra và số lượng quần âu bán ra không vượt quá 2 lần số lượng áo vest bán ra. Khi xuất ra thị trường, 1 chiếc áo vest lãi 350 nghìn đồng, 1 chiếc quần âu lãi 100 nghìn đồng. Gọi x, y lần lượt là số áo vest và quần âu xí nghiệp cần may và bán ra thị trường để xí nghiệp có số tiền lãi cao nhất. Tính giá trị biểu thức $T = 2x + 3y$.
**Câu 6.** Cho $tan \alpha = \frac{2}{3}$. Giá trị của biểu thức $A = \frac{5sin \alpha – 3cos \alpha}{7sin \alpha + 2cos \alpha}$ bằng $\frac{a}{b}$ ( với $a, b \in Z; b \neq 0; \frac{a}{b}$ là phân số tối giản). Tính giá trị biểu thức $T = 100(a + b)$.
Mục đích tổ chức thi tốt nghiệp THPT 2025 là gì?
Căn cứ theo Mục 1 Phương án Tổ chức kỳ thi và xét công nhận tốt nghiệp trung học phổ thông từ năm 2025 ban hành kèm theo Quyết định 4068/QĐ-BGDĐT 2025, mục đích tổ chức thi tốt nghiệp THPT 2025 để:
– Đánh giá đúng kết quả học tập của người học theo mục tiêu và chuẩn cần đạt theo yêu cầu của Chương trình giáo dục phổ thông (GDPT) 2025
– Lấy kết quả thi để xét công nhận tốt nghiệp trung học phổ thông (THPT) và làm một trong các cơ sở để đánh giá chất lượng dạy, học của các cơ sở GDPT và công tác chỉ đạo của các cơ quan quản lý giáo dục.
– Cung cấp dữ liệu đủ độ tin cậy cho các cơ sở giáo dục đại học, giáo dục nghề nghiệp sử dụng trong tuyển sinh theo tinh thần tự chủ.
Thí sinh thi tốt nghiệp THPT 2025 có bắt buộc thi môn Toán học không?
Căn cứ theo Mục 5 Phương án Tổ chức kỳ thi và xét công nhận tốt nghiệp trung học phổ thông từ năm 2025 ban hành kèm theo Quyết định 4068/QĐ-BGDĐT 2025 quy định như sau:
Thí sinh thi bắt buộc môn Ngữ văn, môn Toán và 02 môn thí sinh tự chọn trong số các môn còn lại được học ở lớp 12 (Ngoại ngữ, Lịch sử, Vật lí, Hóa học, Sinh học, Địa lí, Giáo dục kinh tế và pháp luật, Tin học, Công nghệ).
Đồng thời, căn cứ theo Điều 3 Quy chế thi tốt nghiệp trung học phổ thông ban hành kèm theo Thông tư 24/2025/TT-BGDĐT quy định như sau:
Môn thi
Tổ chức kỳ thi gồm 03 buổi thi: 01 buổi thi môn Ngữ văn, 01 buổi thi môn Toán và 01 buổi thi của bài thi tự chọn gồm 02 môn thi trong số các môn: Vật lí, Hóa học, Sinh học, Lịch sử, Địa lí, Giáo dục kinh tế và pháp luật, Tin học, Công nghệ định hướng Công nghiệp (gọi tắt là Công nghệ Công nghiệp), Công nghệ định hướng Nông nghiệp (gọi tắt là Công nghệ Nông nghiệp), Ngoại ngữ (Tiếng Anh, Tiếng Nga, Tiếng Pháp, Tiếng Trung Quốc, Tiếng Đức, Tiếng Nhật và Tiếng Hàn).
Theo quy định này, các môn thi tốt nghiệp THPT 2025 bao gồm:
– Thi 02 môn bắt buộc: Toán và Ngữ văn.
– Thi 02 môn tự chọn trong số các môn sau: Vật lí, Hóa học, Sinh học, Lịch sử, Địa lí, Giáo dục kinh tế và pháp luật, Tin học, Công nghệ định hướng Công nghiệp, Công nghệ định hướng Nông nghiệp, Ngoại ngữ.
Như vậy, kỳ thi tốt nghiệp THPT 2025 bắt buộc thí sinh phải thi môn Toán học.




