Bài tập – Đề thi trắc nghiệm Toán lớp 7 Chương 2 – Bài 1: Số vô tỉ. Căn bậc hai số học là một trong những đề thi thuộc Chương 2 – Số thực trong chương trình Toán lớp 7. Đây là chuyên đề mở đầu quan trọng trong chương số thực, giúp học sinh nhận biết và phân biệt rõ ràng giữa số hữu tỉ và số vô tỉ – một kiến thức nền tảng để tiếp cận sâu hơn với tập hợp số thực R, căn bậc hai, căn bậc ba và nhiều khái niệm đại số khác.
Để làm tốt đề thi lớp 7 này, học sinh cần nắm vững một số nội dung cốt lõi như:
- Khái niệm số vô tỉ, hiểu rằng đó là những số không thể biểu diễn dưới dạng phân số.
- Biết cách xác định căn bậc hai số học của một số không âm.
- Phân biệt giữa các loại căn thức, từ đó chọn đáp án chính xác trong các câu hỏi trắc nghiệm.
Đây là phần kiến thức vô cùng quan trọng vì nó là nền tảng để hiểu các phép biến đổi đại số phức tạp hơn trong những bài học tiếp theo của chương 2.
Hãy cùng Dethitracnghiem.vn cùng tìm hiểu về đề thi này và tham gia làm kiểm tra ngay lập tức!
Bài tập – Đề thi trắc nghiệm Toán lớp 7 Chương 2 – Bài 1
Câu 1. Viết phân số \( \dfrac{16}{15} \) dưới dạng số thập phân vô hạn tuần hoàn ta được:
A. \( 1{,}(06) \)
B. \( 1{,}(07) \)
C. \( 1{,}0(6) \)
D. \( 1{,}067 \)
Câu 2. Chọn phát biểu đúng.
A. Căn bậc hai số học của số \( a \) không âm là số \( x \) không âm sao cho \( x^2 = a \);
B. Căn bậc hai số học của số \( a \) không âm là số \( x \) không âm sao cho \( x^3 = a \);
C. Căn bậc hai số học của số \( a \) không âm là số \( x \) không âm sao cho \( x = a^2 \);
D. Căn bậc hai số học của số \( a \) không âm là số \( x \) không âm sao cho \( x = a^3 \);
Câu 3. Điền hai số thích hợp lần lượt vào chỗ chấm trong câu sau: “Vì \( 5^2 = \ldots \) và \( 5 > 0 \) nên \( \sqrt{\ldots} = 5 \)”.
A. \( 5 \) và \( 5 \);
B. \( 5 \) và \( 25 \);
C. \( 25 \) và \( 5 \);
D. \( 25 \) và \( 25 \).
Câu 4. Tính \( \sqrt{64} \).
A. \( -8 \);
B. \( 8 \);
C. \( \pm 8 \);
D. \( 32 \).
Câu 5. Chọn câu đúng.
A. \( -\sqrt{\dfrac{81}{121}} = \dfrac{9}{11} \)
B. \( -\sqrt{\dfrac{81}{121}} = -\dfrac{9}{11} \)
C. \( -\sqrt{\dfrac{81}{121}} = \pm \dfrac{9}{11} \)
D. Không tính được \( -\sqrt{\dfrac{81}{121}} \)
Câu 6. Giá trị biểu thức \( \sqrt{0{,}16} – \sqrt{0{,}09} \) là:
A. \( 0{,}07 \);
B. \( 0{,}1 \);
C. \( -0{,}1 \);
D. \( -0{,}7 \).
Câu 7. Cho \( a = \sqrt{4 \cdot 25} \) và \( b = \sqrt{4} \cdot \sqrt{25} \). Phát biểu nào sau đây là đúng?
A. \( a < b \);
B. \( a = b \);
C. \( a \ne b \);
D. \( a > b \).
Câu 8. An tính \( \sqrt{100} \) như sau: \( \sqrt{100} = \sqrt{64 + 36} = \sqrt{64} + \sqrt{36} = \sqrt{8^2} + \sqrt{6^2} = 8 + 6 = 14 \). Cô giáo chấm bài của An và nói rằng An đã làm sai. Vậy An đã làm sai ở bước nào?
A. Bước (1);
B. Bước (2);
C. Bước (3);
D. Bước (4).
Câu 9. Giá trị biểu thức \( \dfrac{3}{4} \cdot \sqrt{\dfrac{121}{49}} + \dfrac{ \sqrt{121}}{ \sqrt{49}} \cdot \dfrac{1}{4} \) là:
A. \( -\dfrac{121}{49} \);
B. \( \dfrac{121}{49} \);
C. \( -\dfrac{11}{7} \);
D. \( \dfrac{11}{7} \).
Câu 10. Dùng máy tính cầm tay để tính giá trị của biểu thức \( \sqrt{12{,}5} \) (làm tròn đến hàng phần mười) là:
A. \( 3{,}53 \);
B. \( 3{,}54 \);
C. \( 3{,}5 \);
D. \( 3{,}6 \).
Câu 11. Độ dài cạnh của một hình vuông có diện tích \( 144 \, \text{cm}^2 \) là:
A. \( \pm 12 \, \text{cm} \);
B. \( 12 \, \text{cm} \);
C. \( \pm 72 \, \text{cm} \);
D. \( 72 \, \text{cm} \).
Câu 12. Sau khi sơn tường cho một bức tường hình vuông, bác Phương phải trả cho thợ sơn là 1 280 000 đồng. Biết công thợ sơn cho \( 1 \, \text{m}^2 \) là 20 000 đồng. Độ dài cạnh bức tường đó là:
A. \( 8 \, \text{m} \);
B. \( 32 \, \text{m} \);
C. \( 64 \, \text{m} \);
D. \( 64 \, \text{m}^2 \).
Câu 13. Giá trị \( x \in \mathbb{Q} \) thỏa mãn \( x^2 = 256 \) là:
A. \( x = -16 \);
B. \( x = 16 \);
C. \( x = 16 \) hoặc \( x = -16 \);
D. \( x = 256 \).
Câu 14. Giá trị biểu thức \( \sqrt{6} \cdot \sqrt{6} – 3 \cdot \sqrt{\dfrac{1}{4}} \) là:
A. \( \dfrac{21}{4} \);
B. \( \dfrac{27}{4} \);
C. \( \dfrac{15}{2} \);
D. \( \dfrac{9}{2} \).
Câu 15. Cho hình vuông \( ABCD \) như hình vẽ.
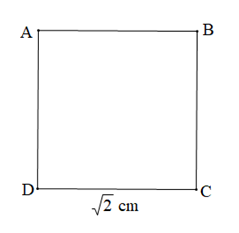
Diện tích hình vuông \( ABCD \) là:
A. \( 2\sqrt{2} \, \text{cm}^2 \);
B. \( \sqrt{2} \, \text{cm}^2 \);
C. \( 2 \, \text{cm}^2 \);
D. \( 4 \, \text{cm}^2 \).




