Bài tập – Đề thi trắc nghiệm Toán lớp 7 Chương 4 – Bài 1: Góc ở vị trí đặc biệt là một trong những đề thi thuộc Chương 4 – Góc. Đường thẳng song song trong chương trình Toán lớp 7. Đây là phần kiến thức cơ bản và rất quan trọng giúp học sinh làm quen với các loại góc đặc biệt như: góc kề bù, góc đối đỉnh, góc phụ nhau, góc bù nhau… cũng như hiểu được mối quan hệ giữa chúng trong các bài toán hình học.
Để làm tốt đề thi lớp 7 này, học sinh cần nắm vững:
- Khái niệm và tính chất của các góc đặc biệt;
- Cách nhận diện vị trí của các góc trên hình vẽ.
Áp dụng linh hoạt các tính chất trong giải toán và chọn đáp án đúng trong đề trắc nghiệm.
Hãy cùng Dethitracnghiem.vn tìm hiểu về đề thi này và tham gia làm kiểm tra ngay lập tức!
Bài tập – Đề thi trắc nghiệm Toán lớp 7 Chương 4 – Bài 1
Câu 1. Chọn đáp án sai. Hai góc kề nhau là:
A. hai góc có đỉnh chung;
B. có một cạnh chung;
C. hai góc không chung đỉnh;
D. có hai cạnh nằm về hai phía của đường thẳng chứa cạnh chung.
Câu 2. Hai góc bù nhau là hai góc có tổng số đo bằng:
A. \( 120^\circ \);
B. \( 90^\circ \);
C. \( 60^\circ \);
D. \( 120^\circ \).
Câu 3. Trong các hình dưới đây hình nào là 2 góc kề bù. 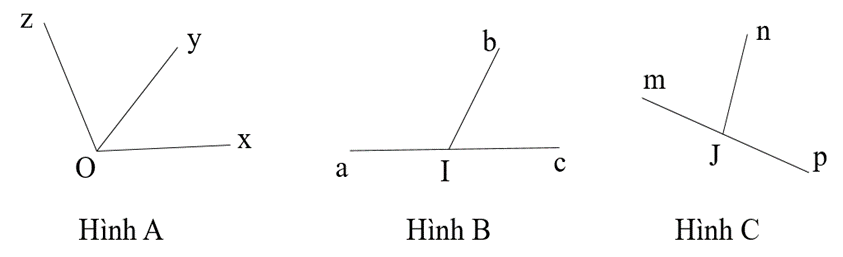
A. Hình A, B;
B. Hình B, C;
C. Hình A, C;
D. Không có hình nào.
Câu 4. Tìm số đo \( x \): 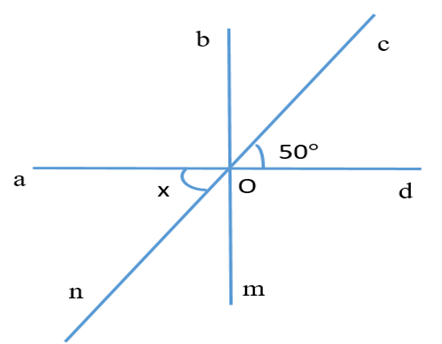
A. \( 40^\circ \);
B. \( 120^\circ \);
C. \( 30^\circ \);
D. \( 50^\circ \).
Câu 5. Hai góc đối đỉnh thì:
A. bằng nhau;
B. có tổng bằng \( 180^\circ \);
C. kề nhau;
D. có hiệu bằng \( 180^\circ \).
Câu 6. Quan sát hình bên và chỉ ra hai góc kề nhau. 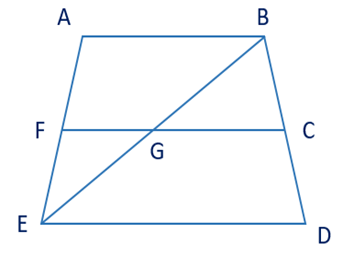
A. góc FGB và góc BGC;
B. góc FGB và góc EGC;
C. góc FAB và góc GBC;
D. góc BGC và góc FGE.
Câu 7. Tìm số đo \( x \) và \( y \) trong hình vẽ dưới đây: 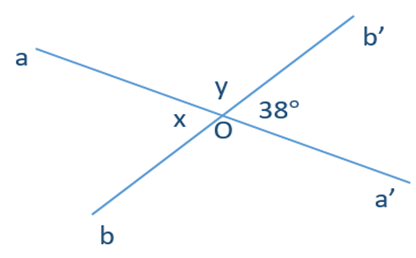
A. \( x = 38^\circ \) và \( y = 52^\circ \);
B. \( x = 38^\circ \) và \( y = 142^\circ \);
C. \( x = 142^\circ \) và \( y = 38^\circ \);
D. \( x = 52^\circ \) và \( y = 38^\circ \).
Câu 8. Chọn đáp án đúng. 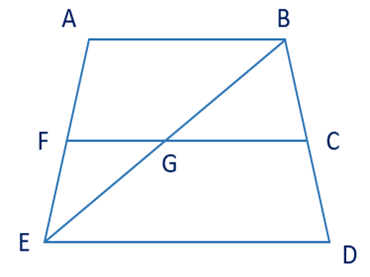
A. \( \widehat{ABC} \) và \( \widehat{CDE} \) là hai góc kề nhau;
B. \( \widehat{BGC} \) và \( \widehat{FGE} \) là hai góc kề nhau;
C. \( \widehat{CGE} \) và \( \widehat{FGB} \) là hai góc kề nhau;
D. \( \widehat{CGE} \) và \( \widehat{EGF} \) là hai góc kề nhau.
Câu 9. Góc \( aOb \) và góc \( b’Oa’ \) là: 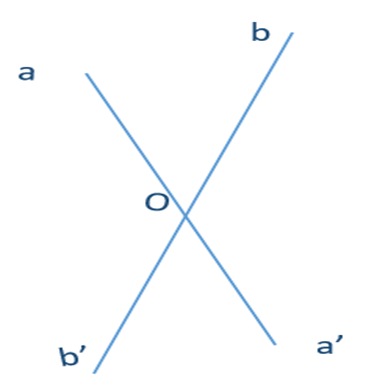
A. hai góc đối đỉnh;
B. hai góc kề nhau;
C. hai góc bù nhau;
D. hai góc kề bù.
Câu 10. Cho hình vẽ. Em hãy chỉ ra 2 góc đối đỉnh (khác góc bẹt). 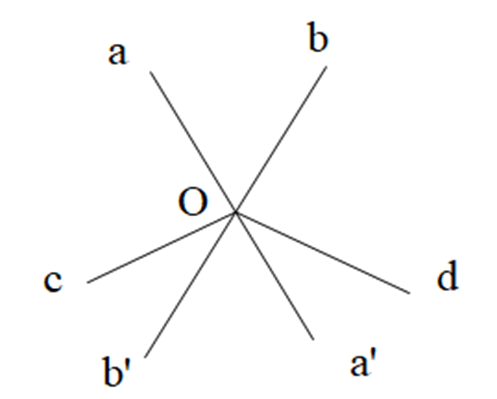
A. \(\widehat{aOb}\) và \(\widehat{aOb’}\);
B. \(\widehat{cOb’}\) và \(\widehat{bOd}\);
C. \(\widehat{aOb}\) và \(\widehat{a’Ob’}\);
D. \(\widehat{aOb’}\) và \(\widehat{aOd}\).
Câu 11. Trong các hình dưới đây hình nào vẽ hai góc kề nhau là không đúng. 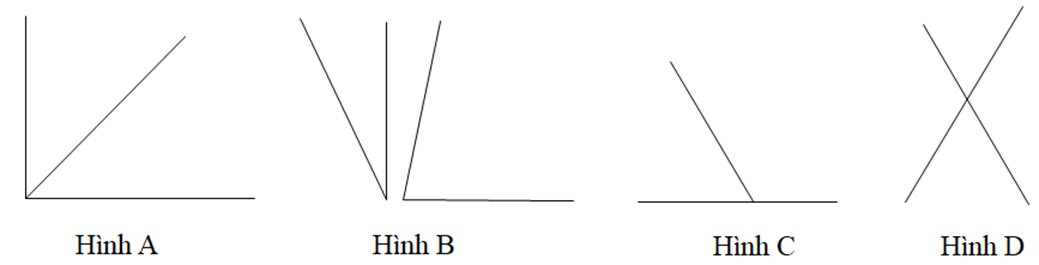
A. Hình A;
B. Hình B;
C. Hình C;
D. Hình D.
Câu 12. Tính góc \( xOz \): 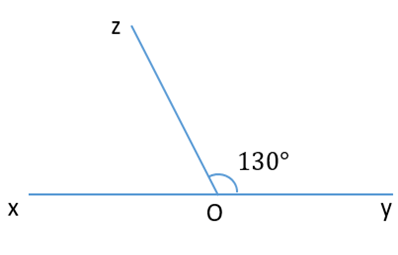
A. \( 70^\circ \);
B. \( 130^\circ \);
C. \( 50^\circ \);
D. \( 120^\circ \).
Câu 13. Trong các hình dưới đây hình nào vẽ hai góc kề bù: 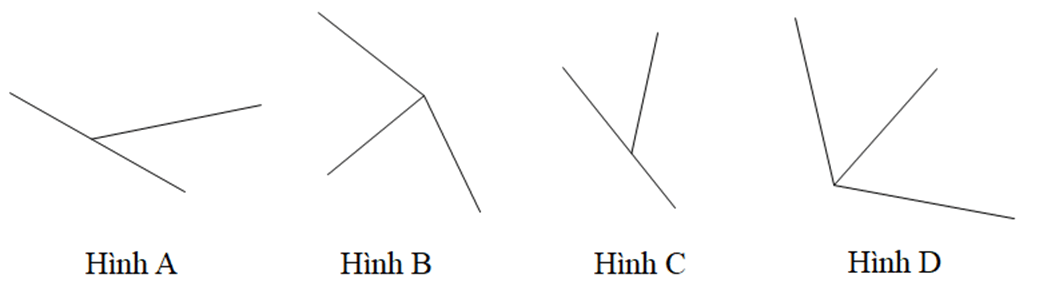
A. Hình A và Hình B;
B. Hình B và Hình C;
C. Hình C và Hình D;
D. Hình A và Hình C.
Câu 14. Chọn câu trả lời đúng.
A. Hai góc bù nhau là hai góc có tổng số đo bằng \( 180^\circ \);
B. Hai góc kề nhau là hai góc có tổng số đo bằng \( 180^\circ \);
C. Hai góc đối đỉnh là hai góc có tổng số đo bằng \( 180^\circ \);
D. Hai góc kề bù là hai góc có tổng số đo bằng \( 90^\circ \).
Câu 15. Cho cặp góc đối đỉnh \( \widehat{tOz} \) và \( \widehat{t’Oz’} \) (Oz và Oz’ là hai tia đối nhau). Biết \( 3\widehat{tOz’} = \widehat{tOz} \). Tính các góc \( \widehat{tOz} \) và \( \widehat{t’Oz’} \).
A. \( \widehat{tOz} = \widehat{t’Oz’} = 45^\circ \);
B. \( \widehat{tOz} = \widehat{t’Oz’} = 105^\circ \);
C. \( \widehat{tOz} = \widehat{t’Oz’} = 135^\circ \);
D. \( \widehat{t’Oz’} = 135^\circ, \; \widehat{tOz} = 45^\circ \).




