Bài tập – Đề thi trắc nghiệm Toán lớp 7 Chương 4 – Ôn tập là một trong những nội dung quan trọng trong chương trình Toán lớp 7, thuộc Chương 4 – Góc. Đường thẳng song song. Đây là giai đoạn tổng hợp toàn bộ kiến thức đã học về các loại góc đặc biệt, tia phân giác, mối quan hệ giữa hai đường thẳng song song và các định lí cơ bản.
Để làm tốt đề thi lớp 7 này, học sinh cần nắm vững các khái niệm then chốt như: góc đối đỉnh, góc kề bù, góc so le trong, góc đồng vị; các dấu hiệu nhận biết hai đường thẳng song song; cách xác định tia phân giác và vận dụng các định lí để giải quyết các bài toán hình học cơ bản.
Đây là một dạng đề kiểm tra lý tưởng giúp học sinh hệ thống lại kiến thức, củng cố kỹ năng suy luận hình học, chuẩn bị tốt cho các bài kiểm tra giữa kỳ và cuối kỳ.
Hãy cùng Dethitracnghiem.vn cùng tìm hiểu về đề thi này và tham gia làm kiểm tra ngay lập tức!
Bài tập – Đề thi trắc nghiệm Toán lớp 7 Chương 4 – Ôn tập
Câu 1. Cho hình vẽ. Tính góc \( \widehat{FEC} \), biết \( EF \parallel BC \) và \( \widehat{ECB} = 40^\circ \): 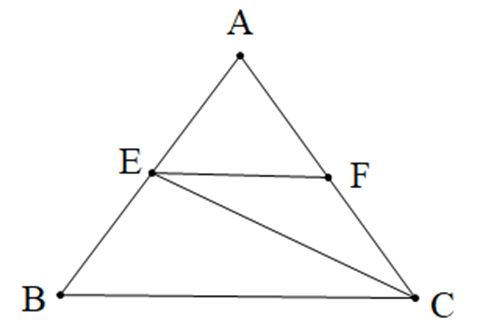
A. \( 50^\circ \);
B. \( 40^\circ \);
C. \( 60^\circ \);
D. \( 30^\circ \).
Câu 2. Cho hình thoi ABCD như hình vẽ. Chọn phương án đúng: 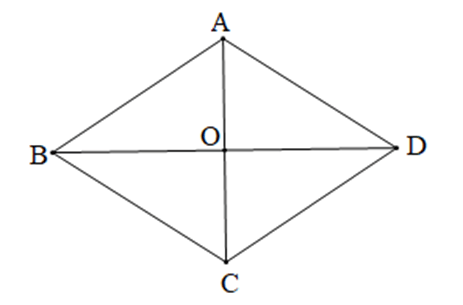
A. \( \widehat{AOB} \) và \( \widehat{DOC} \) là hai góc đối đỉnh;
B. \( \widehat{AOB} \) và \( \widehat{BOC} \) là hai góc so le trong;
C. \( \widehat{BAD} \) và \( \widehat{ADC} \) là hai góc đồng vị;
D. \( \widehat{ABC} \) và \( \widehat{ADC} \) là hai góc kề bù.
Câu 3. Cho hình chữ nhật ABCD như hình vẽ. Biết \( IJ \parallel AB \) và \( \widehat{JOC} = 30^\circ \). Số đo góc \( \widehat{BAC} \) là: 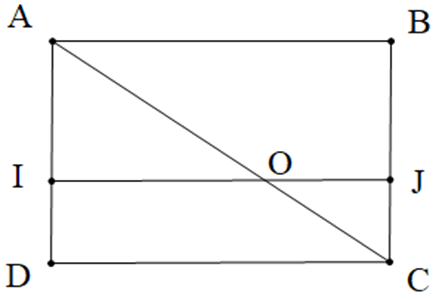
A. \( 60^\circ \);
B. \( 30^\circ \);
C. \( 90^\circ \);
D. \( 80^\circ \).
Câu 4. Cho hình bình hành ABCD như hình vẽ. Biết \( EF \parallel DC \), \( \widehat{DAB} = 65^\circ \) và \( \widehat{AFE} = 35^\circ \). Số đo góc \( \widehat{KAD} \) là: 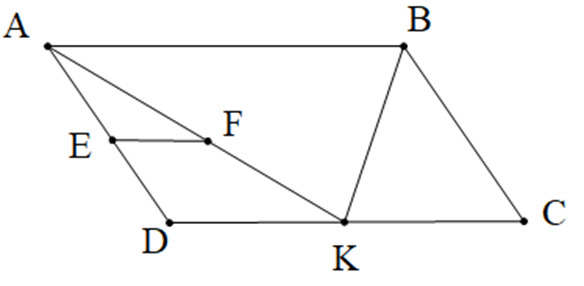
A. \( 60^\circ \);
B. \( 45^\circ \);
C. \( 30^\circ \);
D. \( 125^\circ \).
Câu 5. Cho hình vẽ dưới đây, biết \( a \parallel b \). Tính \( x, y \): 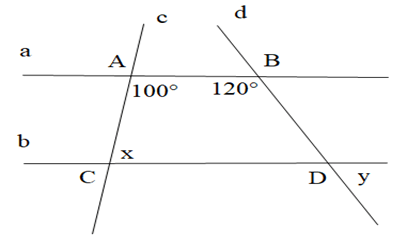
A. \( x = 80^\circ \) và \( y = 80^\circ \);
B. \( x = 60^\circ \) và \( y = 80^\circ \);
C. \( x = 80^\circ \) và \( y = 60^\circ \);
D. \( x = 60^\circ \) và \( y = 60^\circ \).
Câu 6. Cho \( \widehat{mOn} \) và \( \widehat{nOp} \) là hai góc kề bù. Biết \( \widehat{mOn} = 110^\circ \) và Ot là tia phân giác của góc \( \widehat{nOp} \). Số đo góc \( \widehat{mOt} \) là:
A. \( 145^\circ \);
B. \( 135^\circ \);
C. \( 45^\circ \);
D. \( 35^\circ \).
Câu 7. Cho góc AOB và OI là tia phân giác của góc đó. Vẽ tia phân giác OJ của góc BOI. Biết \( \widehat{IOJ} = 25^\circ \). Số đo góc AOB là:
A. \( 120^\circ \);
B. \( 80^\circ \);
C. \( 150^\circ \);
D. \( 100^\circ \).
Câu 8. Cho định lí: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông”. Giả thiết, kết luận của định lí là:
A. Giả thiết: Cho góc bẹt AOB và tia OI; tia OJ là tia phân giác góc BOI, OK là tia phân giác góc AOI. Kết luận: \( \overrightarrow{OI} \perp \overrightarrow{OK} \)
B. Giả thiết: Cho góc bẹt AOB và tia OI; tia OJ là tia phân giác góc BOK, OK là tia phân giác góc AOI. Kết luận: \( \overrightarrow{OI} \perp \overrightarrow{OA} \)
C. Giả thiết: Cho góc bẹt AOB và tia OI; tia OJ là tia phân giác góc BOI, OK là tia phân giác góc AOK. Kết luận: \( \overrightarrow{OI} \perp \overrightarrow{OK} \)
D. Giả thiết: Cho góc bẹt AOB và tia OI; tia OJ là tia phân giác góc BOI, OK là tia phân giác góc AOI. Kết luận: \( \overrightarrow{OB} \perp \overrightarrow{OK} \)
Câu 9. Khi chứng minh định lí, người ta cần:
A. Chứng minh định lí đó đúng trong một trường hợp cụ thể của giả thiết;
B. Chứng minh định lí đó đúng trong hai trường hợp cụ thể của giả thiết;
C. Chứng minh định lí đó đúng trong mọi trường hợp có thể xảy ra của giả thiết;
D. Chứng minh định lí đó đúng trong vài trường hợp cụ thể của giả thiết.
Câu 10. Cho các phát biểu sau: (1) Hai góc đối đỉnh thì bằng nhau; (2) Hai bằng nhau thì đối đỉnh; (3) Hai đường thẳng song song thì cắt nhau; (4) Nếu N là trung điểm của HK thì \( NH = NK \); (5) Nếu \( NH = NK \) thì N là trung điểm của HK. Có bao nhiêu phát biểu đúng?
A. 1;
B. 2;
C. 3;
D. 5.
Câu 11. Cho hình vẽ. Góc \( \widehat{AOI} \) và góc \( \widehat{IOB} \) là: 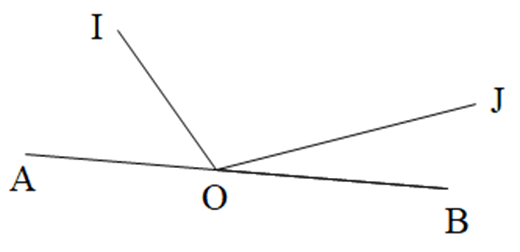
A. hai góc đối đỉnh;
B. hai góc kề bù;
C. hai góc so le trong;
D. hai góc đồng vị.
Câu 12. Cho hình vẽ. Biết OI là tia phân giác góc \( \widehat{AOB} \). Số đo góc \( \widehat{AOI} \) là: 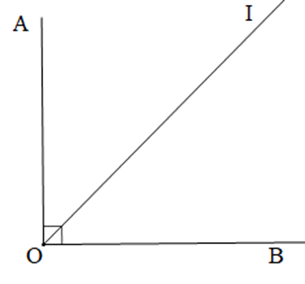
A. \( 40^\circ \);
B. \( 45^\circ \);
C. \( 60^\circ \);
D. \( 65^\circ \).
Câu 13. Cho hình vẽ sau. Chọn đáp án đúng: 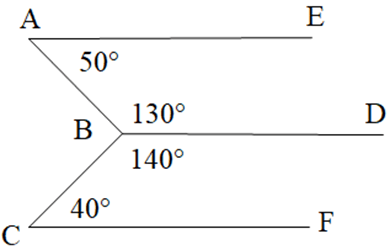
A. AE // BD;
B. BD // CF;
C. Cả A và B đều sai;
D. Cả A và B đều đúng.
Câu 14. Hai đường thẳng xy và x’y’ cắt nhau tại O. Góc đối đỉnh của \( \widehat{xOy’} \) là:
A. \( \widehat{x’Oy’} \);
B. \( \widehat{x’Oy} \);
C. \( \widehat{xOy’} \);
D. \( \widehat{xOy} \).
Câu 15. Cho ba đường thẳng phân biệt a, b và c, biết \( a // b \) và \( a \perp c \). Kết luận nào đúng:
A. \( b // c \);
B. \( b \perp c \);
C. \( a \perp b \);
D. Cả 3 đáp án đều sai.
Câu 16. Trong các hình dưới đây hình nào là 2 góc kề bù. 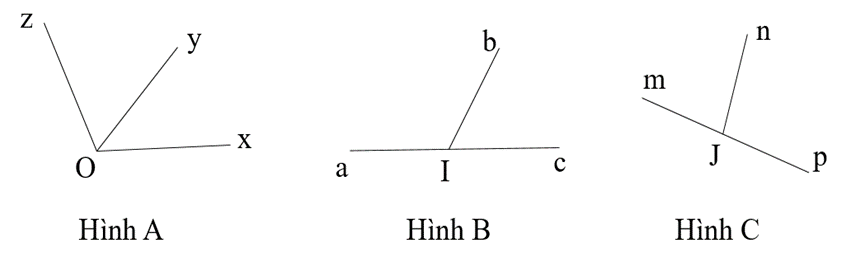
A. Hình A, B;
B. Hình B, C;
C. Hình A, C;
D. Không có hình nào.
Câu 17. Tìm số đo \( x \). 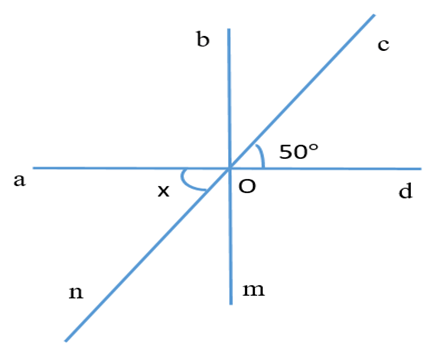
A. \( 40^\circ \);
B. \( 120^\circ \);
C. \( 30^\circ \);
D. \( 50^\circ \).
Câu 18. Định lí: “Nếu hai đường thẳng song song cùng cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau”. Giả thiết của định lí là:
A. \( a // b;\ a // c \)
B. \( a // c;\ b\ \text{bất kỳ} \)
C. \( a // b;\ a \perp c \)
D. \( a // b;\ c \cap a = (M);\ c \cap b = (N) \)
Câu 19. Tìm số đo \( x \) và \( y \) trong hình vẽ dưới đây: 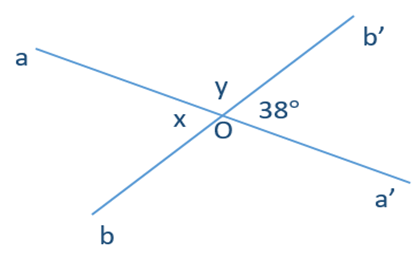
A. \( x = 38^\circ,\ y = 52^\circ \)
B. \( x = 38^\circ,\ y = 142^\circ \)
C. \( x = 142^\circ,\ y = 38^\circ \)
D. \( x = 52^\circ,\ y = 38^\circ \)
Câu 20. Chọn đáp án đúng. 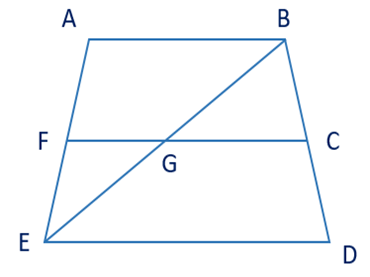
A. \( \angle ABC \text{ và } \angle CDE \text{ là hai góc kề nhau;} \)
B. \( \angle BGC \text{ và } \angle FGE \text{ là hai góc kề nhau;} \)
C. \( \angle CGE \text{ và } \angle FGB \text{ là hai góc kề nhau;} \)
D. \( \angle CGE \text{ và } \angle EGF \text{ là hai góc kề nhau.} \)
Câu 21. Chọn phát biểu đúng.
A. Giả thiết của định lí là điều suy ra;
B. Kết luận của định lí là điều cho biết;
C. Giả thiết của định lí là điều cho biết;
D. Cả A và B đều đúng.
Câu 22. Cho định lí: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại”. Hình vẽ minh hoạ cho định lí trên là:
A. 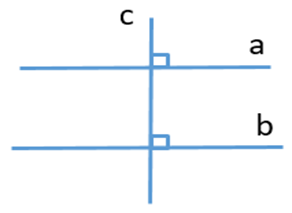
B. 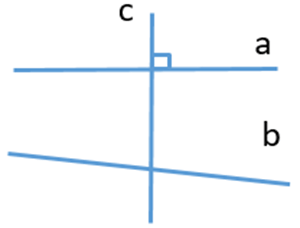
C. 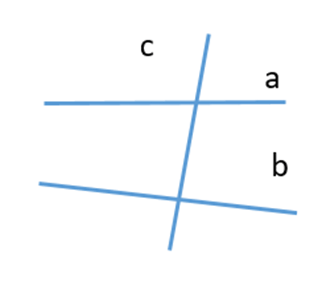
D. 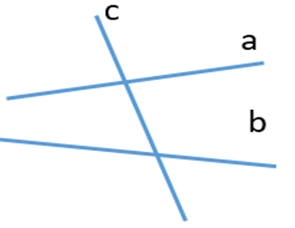
Câu 23. Viết giả thiết cho định lí sau: “Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì hai đường thẳng đó song song với nhau”.
A. Giả thiết: \( a \ne b; \, a \parallel c, \, b \parallel c \)
B. Giả thiết: \( a \equiv b; \, a \parallel b, \, b \parallel c \)
C. Giả thiết: \( a \equiv b; \, a \perp c, \, b // c \)
D. Giả thiết: \( a \ne b; \, a \perp c, \, b // c \)
Câu 24. Chọn phát biểu đúng. 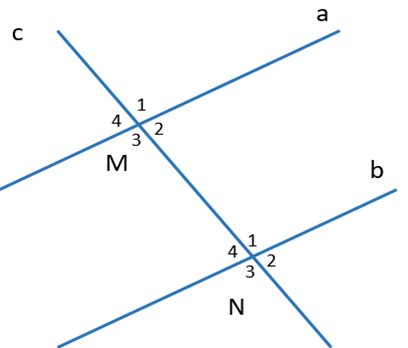
A. \( \widehat{M_1} \) và \( \widehat{N_1} \) là hai góc so le trong
B. \( \widehat{M_2} \) và \( \widehat{N_2} \) là hai góc so le ngoài
C. \( \widehat{M_3} \) và \( \widehat{N_1} \) là hai góc đồng vị
D. \( \widehat{M_4} \) và \( \widehat{N_4} \) là hai góc đồng vị
Câu 25. Chọn một cặp góc đồng vị trong hình vẽ sau: 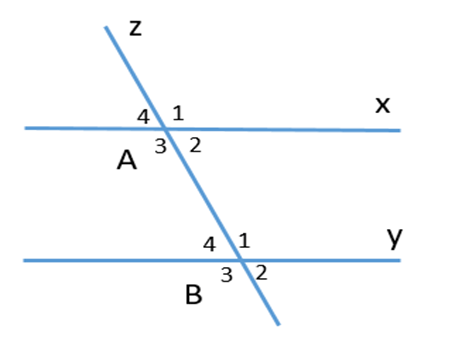
A. \( \widehat{B_2} \) và \( \widehat{B_3} \)
B. \( \widehat{A_3} \) và \( \widehat{B_3} \)
C. \( \widehat{A_2} \) và \( \widehat{B_4} \)
D. \( \widehat{A_4} \) và \( \widehat{A_2} \)
Câu 26. Nếu đường thẳng \( z \) cắt hai đường thẳng \( x \), \( y \) và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
A. hai đường thẳng \( x, y \) song song với nhau;
B. hai đường thẳng \( x, y \) cắt nhau;
C. hai đường thẳng \( x, y \) trùng nhau;
D. hai đường thẳng \( x, y \) vuông góc với nhau.
Câu 27. Chọn hình vẽ. Em hãy chọn câu trả lời đúng: 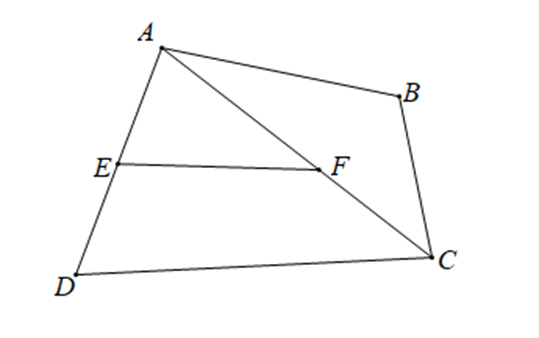
A. \( \widehat{DAC} \) và \( \widehat{AFE} \) là hai góc so le trong;
B. \( \widehat{AFE} \) và \( \widehat{BAC} \) là hai góc so le trong;
C. \( \widehat{AFE} \) và \( \widehat{ADC} \) là hai góc đồng vị;
D. \( \widehat{BAC} \) và \( \widehat{DAC} \) là hai góc đồng vị.
Câu 28. Cho hình vẽ. Biết \( \widehat{xOz} = 30^\circ \), Oz là tia phân giác của góc xOy. Số đo của góc xOy là: 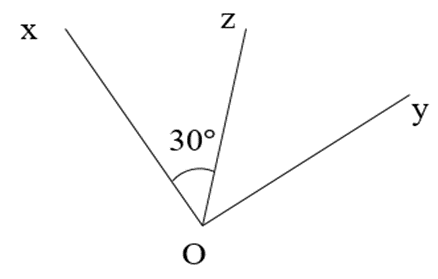
A. \( 30^\circ \)
B. \( 60^\circ \)
C. \( 120^\circ \)
D. \( 140^\circ \)
Câu 29. Cho \( \widehat{HOK} = 90^\circ \) và tia OK là tia phân giác của góc HOI. Khi đó góc HOI là:
A. góc vuông;
B. góc nhọn;
C. góc tù;
D. góc bẹt.
Câu 30. Cho \( \widehat{xOy} = 120^\circ \), tia Ot là tia phân giác của góc xOy. Tính số đo góc xOt:
A. \(120^\circ\)
B. \(80^\circ\)
C. \(60^\circ\)
D. \(150^\circ\)




