Trắc nghiệm Toán 11: Bài 27 – Thể tích là một phần quan trọng trong chương trình Toán 11, thuộc chương VII: Quan hệ vuông góc trong không gian. Trong bài học này, học sinh sẽ tìm hiểu các kiến thức cơ bản về thể tích của các hình khối trong không gian như hình lập phương, hình chóp, hình cầu, và các phép tính liên quan đến thể tích trong không gian ba chiều. Để giải quyết các bài toán về thể tích, học sinh cần nắm vững các công thức tính thể tích của từng loại hình khối, cùng với khả năng vận dụng các định lý và phương pháp giải tích không gian.
Một số trọng tâm cần nắm trong bài này bao gồm:
- Công thức tính thể tích của các khối hình như hình chóp, hình lập phương, hình cầu.
- Cách tính thể tích thông qua tích vô hướng của các vectơ trong không gian.
- Sử dụng các công thức xác định thể tích trong các bài toán thực tế.
Hãy cùng Dethitracnghiem.vn tìm hiểu về đề thi này và tham gia làm kiểm tra ngay lập tức để củng cố kiến thức của mình!
Trắc nghiệm Toán 11: Bài 27 – Thể tích
Câu 1: Cho hình hộp chữ nhật ABCD.A’B’C’D’ đáy là hình chữ nhật có AB = 2a, AD = 6a. Gọi M là trung điểm của AD, biết khoảng cách từ C đến mặt phẳng (A’BM) bằng \(\dfrac{12a}{7}\). Thể tích khối hộp ABCD.A’B’C’D’ là
A. \(24a^3\)
B. \(12a^3\)
C. \(3a^3\)
D. \(8a^3\)
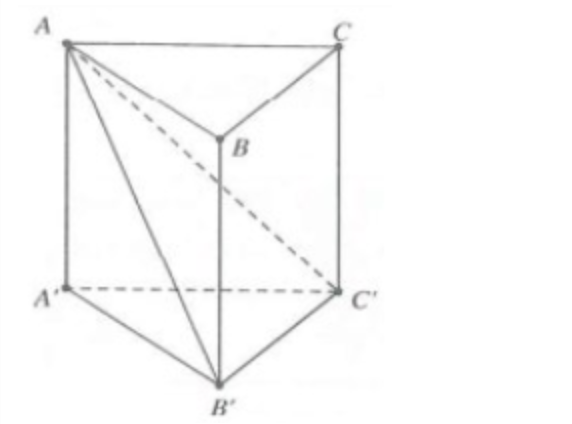
Câu 2: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông, AB = BC = a. Biết rằng góc giữa hai mặt phẳng (ACC’) và (AB’C’) bằng \(60^\circ\). Thể tích của khối chóp B’.ACC’A’ bằng:
A. \(\dfrac{a^3}{3}\)
B. \(\dfrac{a^3}{6}\)
C. \(\dfrac{a^3}{2}\)
D. \(\dfrac{a^3\sqrt{3}}{3}\)
Câu 3: Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B có \(AB = a\sqrt{3}, BC = a\). Tam giác SAC cân tại S và thuộc mặt phẳng vuông góc với đáy, mp(SAB) tọ với đáy một góc bằng \(60^\circ\). Thể tích khối chóp S.ABC là
A. \(\dfrac{a^3\sqrt{3}}{3}\)
B. \(\dfrac{a^3\sqrt{2}}{3}\)
C. \(\dfrac{a^3}{4}\)
D. \(2a^3\)
Câu 4: Khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác ABC có \(\widehat{BAC} = 120^\circ\), AB = 3a và AC = 4a. Gọi M là trung điểm của B’C’, biết khoảng cách từ M đến mặt phẳng (B’AC) bằng \(\dfrac{3\sqrt{15}}{10}\). Thể tích khối lăng trụ đã cho là
A. \(a^3\)
B. \(9a^3\)
C. \(4a^3\)
D. \(27a^3\)
Câu 5: Cho hình lăng trụ ABC.A’B’C’ có tam giác ABC vuông tại B, có AB = a, AC = 2a. Tam giác A’AC cân tịa A’ và A’ thuộc mặt phẳng vuông góc với đáy. Mặt phẳng (A’AC) tạo với đáy một góc \(45^\circ\). Thể tích khối lăng trụ ABC.A’B’C’ là
A. \(\dfrac{2a^3\sqrt{3}}{3}\)
B. \(\dfrac{a^3\sqrt{3}}{12}\)
C. \(\dfrac{a^3\sqrt{6}}{3}\)
D. \(\dfrac{a^3\sqrt{4}}{3}\)
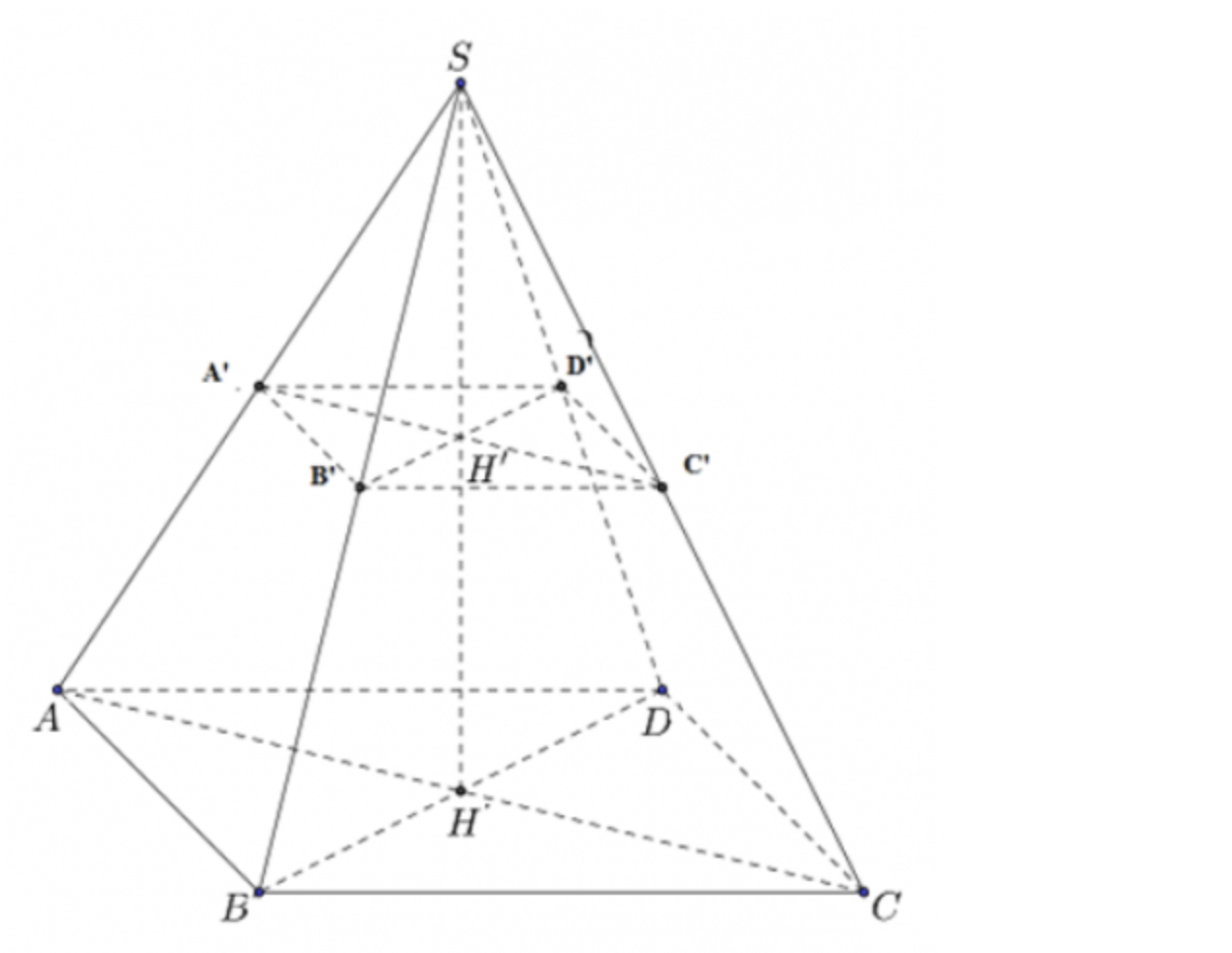
Câu 6: Cho hình chóp tứ giác đều S.ABCD có đường cao SH = 6cm, cạnh đáy bằng 4cm. Một mặt phẳng đi qua trung điểm H’ của SH và song song với đáy và cắt mặt bên của hình chóp tạo thành hình chóp nhỏ S.A’B’C’D’ và hình chóp cụt (tham khảo hình vẽ). Tính thể tích của hình chóp cụt ABCD.A’B’C’D’.
A. \(16 cm^3\)
B. \(28 cm^3\)
C. \(30 cm^3\)
D. \(4 cm^3\)
Câu 7: Cho khối trụ ABC.A’B’C’ có đáy là tam giác ABC vuông tại B có AB = BC = 2a. Biết rằng hình chiếu A’ lên mặt đáy trùng với trọng tâm tam giác ABC. Biết \(A’C = \dfrac{2\sqrt{14}}{3}\). Thể tích khối lăng trụ đã cho là
A. \(2a^3\)
B. \(4a^3\)
C. \(8a^3\)
D. \(4a^3\sqrt{3}\)
Câu 8: Cho khối lăng trụ ABC.A’B’C’ có đáy là tam giác ABC đều cạnh 6a. Hình chiếu vuông góc của đỉnh A’ xuống mặt phẳng đáy thuộc cạnh AC sao cho HC = 2HA. Biết khoảng cách từ C đến mặt phẳng (ABB’A’) bằng \(\dfrac{9a}{2}\). Thể tích khối lăng trụ ABC.A’B’C’ là
A. \(18a^3\sqrt{3}\)
B. \(36a^3\sqrt{3}\)
C. \(54a^3\sqrt{3}\)
D. \(27a^3\sqrt{3}\)
Câu 9: Cho hình chóp S.ABC có đáy la tam giác ABC, các cạnh bên SA = SB = SC = a. Biết rằng \(\widehat{ASB} = 60^\circ, \widehat{BSC} = 90^\circ, \widehat{ASC} = 120^\circ\). Thể tích khối chóp đã cho
A. \(V = \dfrac{a^3\sqrt{6}}{3}\)
B. \(\dfrac{a^3\sqrt{6}}{2}\)
C. \(\dfrac{a^3\sqrt{12}}{2}\)
D. \(\dfrac{a^3\sqrt{12}}{3}\)
Câu 10: Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a, cạnh bên tạo với đáy một góc bằng \(60^\circ\). Tính thể tích khối chóp đã cho
A. \(\dfrac{a^3\sqrt{3}}{4}\)
B. \(\dfrac{a^3\sqrt{3}}{8}\)
C. \(\dfrac{a^3\sqrt{3}}{12}\)
D. \(\dfrac{a^3\sqrt{3}}{24}\)
Câu 11: Cho hình chóp S.ABC có đáy là tam giác ABC, có AB = AC = a, \(\widehat{BAC} = 120^\circ\). Các cạnh bên đều tạo với đáy một góc \(60^\circ\). Thể tích khối chóp S.ABC là
A. \(V = \dfrac{a^3}{4}\)
B. \(V = \dfrac{a^3\sqrt{3}}{4}\)
C. \(V = \dfrac{a^3\sqrt{3}}{8}\)
D. \(V = \dfrac{a^3\sqrt{3}}{12}\)
Câu 12: Cho hình chóp S.ABC có đáy là tam giác ABC có AB = AC = 2a và \(BC = 2a\sqrt{3}\), gọi M là trung điểm của BC. Tam giác SAM cân tại S và thuộc mặt phẳng vuông góc với đáy. Khoảng cách từ A đến mặt phẳng (SBC) bằng \(\dfrac{a\sqrt{3}}{2}\). Thể tích khối chóp S.ABC là
A. \(\dfrac{a^3}{6}\)
B. \(\dfrac{a^3}{2}\)
C. \(\dfrac{3a^3}{2}\)
D. \(\dfrac{a^3\sqrt{2}}{3}\)
Câu 13: Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B có AB = 3, BC = 4. Biết rằng các mặt bên của khối chóp đều tạo với đáy một góc bằng \(60^\circ\). Thể tích khối chóp đã cho là
A. \(V = 5\sqrt{3}\)
B. \(V = 5\sqrt{6}\)
C. \(V = 5\sqrt{2}\)
D. \(V = 5\sqrt{12}\)
Câu 14: Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh bên gấp hai lần cạnh đáy. Tính thể tích V của khối chóp đã cho
A. \(V = \dfrac{a^3\sqrt{14}}{6}\)
B. \(V = \dfrac{a^3\sqrt{2}}{2}\)
C. \(V = \dfrac{a^3\sqrt{14}}{2}\)
D. \(V = \dfrac{a^3\sqrt{2}}{14}\)
Câu 15: Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a. Biết rằng hình chiếu vuông góc A’ xuống đáy trùng với trung điểm của AB và \(AC’ = \dfrac{3a}{2}\). Thể tích khối lăng trụ đã cho là
A. \(\dfrac{a^3}{4}\)
B. \(\dfrac{a^3}{12}\)
C. \(\dfrac{a^3\sqrt{3}}{4}\)
D. \(\dfrac{a^3\sqrt{3}}{12}\)
Câu 16: Cho hình chóp tứ giác đều S.ABCD có đường cao SH = 6cm, cạnh đáy bằng 6cm. Lấy điểm H’ ∈ SH sao cho \(SH’ = \dfrac{2}{3}SH\). Một mặt phẳng đi qua H’ và song song với đáy và cắt mặt bên của hình chóp tạo thành hình chóp nhỏ S.A’B’C’D’ và hình chóp cụt ABCD.A’B’C’D’. Tính thể tích của hình chóp cụt ABCD.A’B’C’D’.
A. \(16 cm^3\)
B. \(50 cm^3\)
C. \(64 cm^3\)
D. \(\dfrac{152}{3} cm^3\)
Câu 17: Cho hình lăng trụ ABC.A’B’C’ biết C’.ABC là hình chóp tam giác đều có đường cao bằng h. Đường thẳng AA’ tạo với đáy một góc \(60^\circ\). Thể tích khối lăng trụ đã cho tính theo h là
A. \(\dfrac{h^3\sqrt{3}}{8}\)
B. \(\dfrac{h^3\sqrt{3}}{4}\)
C. \(\dfrac{h^3\sqrt{3}}{2}\)
D. \(\dfrac{3h^3}{4}\)
Câu 18: Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A’ xuống đáy là trung điểm của AB. Biết khoảng cách từ A đến mặt phẳng (A’BC) bằng \(\dfrac{a\sqrt{15}}{5}\). Thể tích khối lăng trụ ABC.A’B’C’ là
A. \(\dfrac{3a^3}{8}\)
B. \(\dfrac{3a^3}{4}\)
C. \(\dfrac{a^3}{8}\)
D. \(\dfrac{a^3\sqrt{3}}{8}\)
Câu 19: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình chữ nhật ABCD có AB = 3a, AD = 4a. Đường thẳng A’C tạo với mặt phẳng (A’B’BA) một góc \(30^\circ\). Tính thể tích khói hộp chữ nhật đã cho là
A. \(2a^3\sqrt{39}\)
B. \(18a^3\sqrt{39}\)
C. \(a^3\sqrt{39}\)
D. \(6a^3\sqrt{39}\)
Câu 20: Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a, mặt bên tạo với đáy một góc bằng \(60^\circ\). Tính thể tích khối chóp đã cho
A. \(\dfrac{a^3\sqrt{3}}{4}\)
B. \(\dfrac{a^3\sqrt{3}}{8}\)
C. \(\dfrac{a^3\sqrt{3}}{12}\)
D. \(\dfrac{a^3\sqrt{3}}{24}\)




