Trắc nghiệm Toán 11 Bài 20 – Hàm số mũ và hàm số lôgarit là một trong những đề thi thuộc Chương VI – Hàm số mũ và hàm số lôgarit trong chương trình Toán 11. Đây là nội dung quan trọng, giúp học sinh hiểu sâu hơn về hai loại hàm số đặc biệt: hàm số mũ và hàm số lôgarit – vốn có ứng dụng rộng rãi trong thực tế và là nền tảng quan trọng trong chương trình toán lớp 12 và đại học sau này.
Ở Bài 20: Hàm số mũ và hàm số lôgarit, học sinh cần nắm được tập xác định, tính đơn điệu, giới hạn, sự liên tục và đồ thị của các hàm số này. Bên cạnh đó, việc so sánh, biện luận và áp dụng các tính chất đặc trưng của từng loại hàm vào giải các bài toán trắc nghiệm cũng là trọng tâm cần được chú ý. Đây là dạng bài đòi hỏi tư duy linh hoạt, kỹ năng xử lý nhanh và khả năng nhận biết dạng toán chính xác.
Hãy cùng Dethitracnghiem.vn cùng tìm hiểu về đề thi này và tham gia làm kiểm tra ngay lập tức!
Trắc nghiệm Toán 11 Bài 20 – Hàm số mũ và hàm số lôgarit
Câu 1: Tìm tập xác định D của hàm số \(y = \log_2\sqrt{x+1} – \log_{\frac{1}{2}}(3-x) – \log_3(x-1)^3\)
A. D = (1; 3)
B. D = (-1; 1)
C. \(D=(-\infty;3)\)
D. \(D=(1;+\infty)\)
Câu 2: Tìm tập xác định D của hàm số \(y = \log_2(x^2 – 2x – 3)\)
A. \(D=(-\infty;-1]\cup[3;+\infty)\)
B. D = [-1;3]
C. \(D=(-\infty;-1)\cup(3;+\infty)\)
D. D = (-1;3)
Câu 3: Đường cong trong hình sau là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
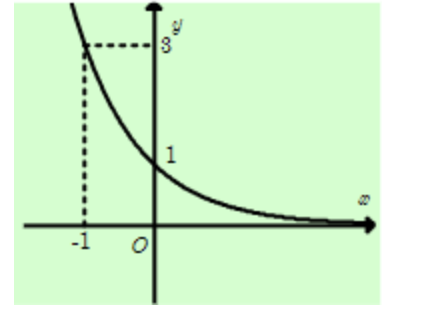
A. \(y=(\sqrt{3})^x\)
B. \(y=(\frac{1}{2})^x\)
C. \(y=2^{x+\frac{5}{2}}\)
D. \(y=(\frac{1}{3})^x\)
Câu 4: Cho hàm số \(f(x) = 2017^x\). Tính \(P = f(x)f(x+1)f(x+2)f(3x)\)
A. \(P = 2017^x\)
B. P = 3.2017
C. P = 3
D. \(P = 2017^3\)
Câu 5: Cho các hàm số \(y = \log_a x\) và \(y = \log_b x\) có đồ thị như hình vẽ. Đường thẳng x = 5 cắt trục hoành, đồ thị hàm số \(y = \log_a x\) và \(y = \log_b x\) lần lượt tại A, B và C. Biết rằng CB = 2AB. Mệnh đề nào sau đây đúng?
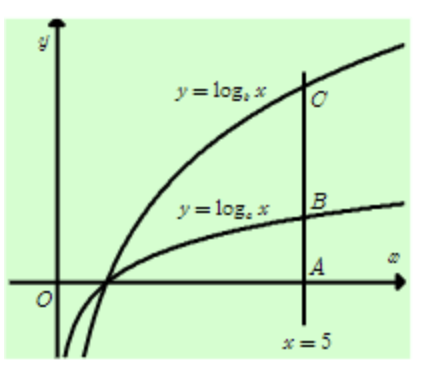
A. \(a = b^2\)
B. \(a^3 = b\)
C. \(a = b^3\)
D. a = 5b
Câu 6: Cho hàm số \(f(x) = \frac{4^x}{4^x + 2}\). Tính tổng \(S = f(\frac{1}{2017}) + f(\frac{2}{2017}) + … + f(\frac{2016}{2017})\)
A. S = 2016
B. S = 1008
C. S = 1007
D. S = 2017
Câu 7: Cho hàm số \(f(x) = \frac{9^x}{9^x + 3}\). Tính tổng \(S = f(\frac{1}{2017}) + f(\frac{2}{2017}) + … + f(\frac{2016}{2017})\)
A. S = 2016
B. S = 1008
C. S = 1007
D. S = 2017
Câu 8: Đường cong trong hình sau là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
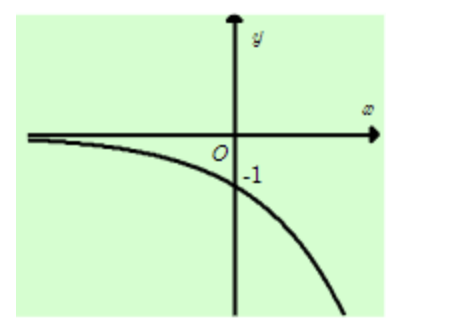
A. \(y = -2^x\)
B. \(y = (\frac{1}{2})^x\)
C. \(y = 2^x\)
D. \(y = -(\frac{1}{2})^x\)
Câu 9: Cho \(9^x + 9^{-x} = 23\). Tính giá trị biểu thức \(P = \frac{5 + 3^x + 3^{-x}}{1 – 3^x – 3^{-x}}\)
A. P = 2
B. \(P = \frac{3}{2}\)
C. \(P = \frac{1}{2}\)
D. \(P = \frac{5}{2}\)
Câu 10: Tìm tất cả các giá trị thực của tham số m để hàm số \(y = ln(x^2 – 2mx + m)\) có tập xác định là R
A. m < 0; m > 1
B. 0 < m < 1
C. \(m \le 0; m \ge 1\)
D. \(0 \le m \le 1\)
Câu 11: Tìm tập xác định D của hàm số \(y = \log_2 \frac{x-1}{x}\)
A. D = (0; 1)
B. \(D=(1;+\infty)\)
C. D = R \ {0}
D. \(D=(-\infty;0)\cup(1;+\infty)\)
Câu 12: Tìm tập xác định D của hàm số \(y = \sqrt{\log_2(x+1) – 1}\)
A. \(D=(-\infty;1]\)
B. \(D=(3;\infty)\)
C. \(D=[1;+\infty)\)
D. D = R \ {3}
Câu 13: Đường cong trong hình sau là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
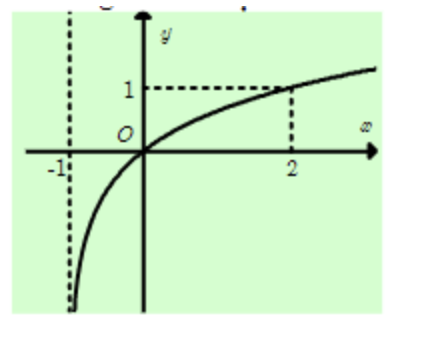
A. \(y = \log_2 x\)
B. \(y = \log_2 (x+1)\)
C. \(y = \log_3 x + 1\)
D. \(y = \log_3 (x+1)\)
Câu 14: Cho số tực x thỏa mãn \(\log_2[4\log_4(8\log_2 x)] = 8\). Tính lnx
A. \(lnx = 2^{125}.ln2\)
B. \(lnx = 2^{126}.ln2\)
C. \(lnx = 2^{127}.ln2\)
D. \(lnx = 2^{128}.ln2\)
Câu 15: Tìm tập xác định của hàm số \(y = \log_5 \frac{x-3}{x+2}\)
A. D = (-2; 3)
B. \(D=(-\infty;-2)\cup[3;+\infty)\)
C. D = R \ {-2}
D. \((-\infty;-2)\cup(3;+\infty)\)
Câu 16: Cho hàm số \(y = (\sqrt{2})^x\) có đồ thị Hình 1. Đồ thị Hình 2 là của hàm số nào dưới đây
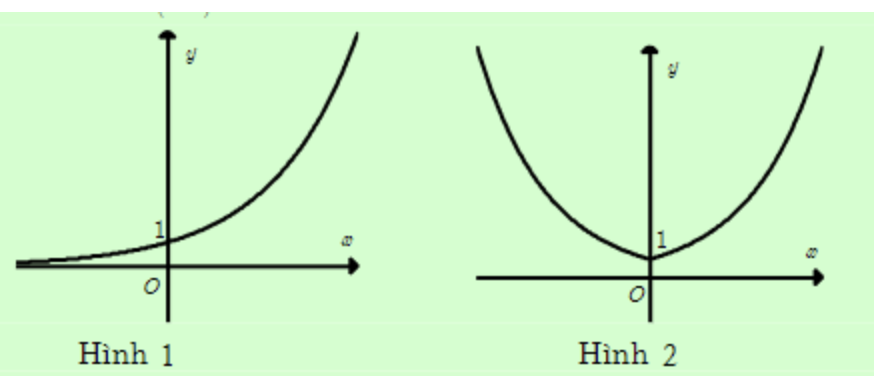
A. \(y = |(\sqrt{2})^x|\)
B. \(y = -(\sqrt{2})^x\)
C. \(y = (\sqrt{2})^{|x|}\)
D. \(y = -|(\sqrt{2})^x|\)
Câu 17: Cho hàm số \(f(x) = \frac{4^x}{4^x + 2}\) và góc \(\alpha\) tùy ý. Tính \(S = f(sin^2 \alpha) + f(cos^2 \alpha)\)
A. S = 1
B. S = 2
C. S = 3
D. \(S = 4sin^2 \alpha\)
Câu 18: Cho hàm số y = lnx có đồ thị Hình 1. Đồ thị Hình 2 là của hàm số nào dưới đây?
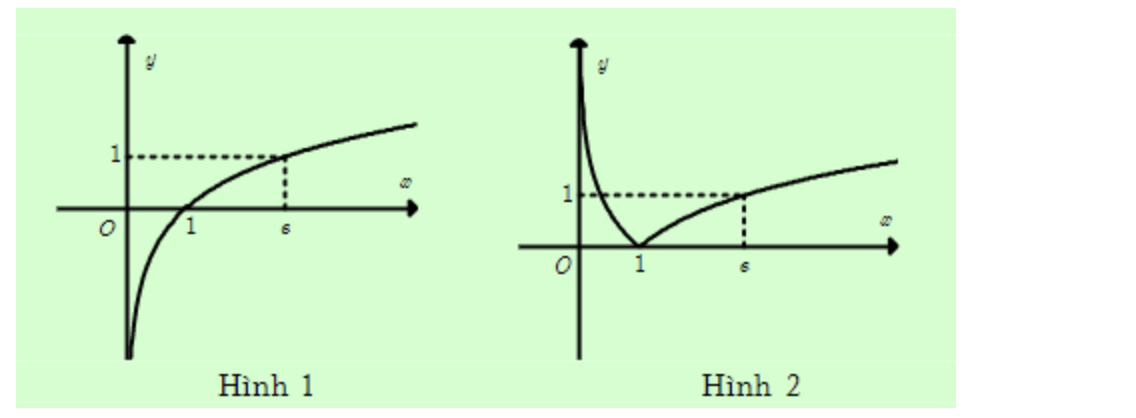
A. y = ln|x|
B. y = |lnx|
C. y = |ln(x + 1)|
D. y = ln|x + 1|
Câu 19: Cho hàm số \(f(x) = \frac{9^x}{9^x + 3}\). Biết a + b = 3, tính S = f(a) + f(b – 2)
A. S = 1
B. S = 2
C. \(S = \frac{1}{4}\)
D. \(S = \frac{3}{4}\)
Câu 20: Cho đồ thị của ba hàm số \(y = x^\alpha\), \(y = x^\beta\), \(y = x^\gamma\) trên khoảng (0;+∞) trên cùng một hệ trục tọa độ như hình vẽ. Mệnh đề nào sau đây đúng
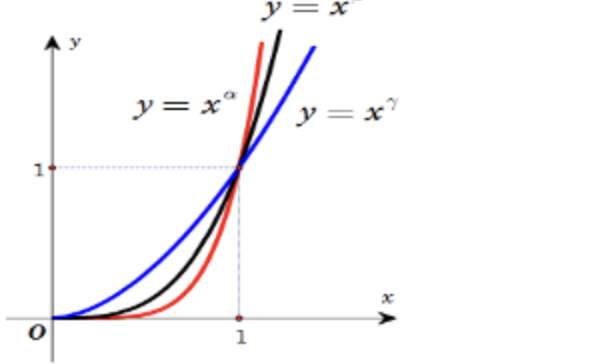
A. \(\gamma < \beta < \alpha < 0\)
B. \(0 < \gamma < \beta < \alpha < 1\)
C. \(1 < \gamma < \beta < \alpha\)
D. \(0 < \alpha < \beta < \gamma < 1\)




