Trắc nghiệm Toán 11: Bài 24 – Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng là một trong những đề thi thuộc chương VII – Quan hệ vuông góc trong không gian trong chương trình Toán 11, với trọng tâm là kỹ thuật dựng hình và tính toán liên quan đến góc và khoảng cách trong không gian.
Trong bài học này, học sinh sẽ được tiếp cận với hai khái niệm quan trọng: phép chiếu vuông góc và góc giữa đường thẳng và mặt phẳng – những nội dung cốt lõi giúp giải quyết các bài toán hình học không gian ở mức độ vận dụng và vận dụng cao. Các kiến thức cần nắm bao gồm:
- Cách dựng hình chiếu vuông góc của một điểm hay một đường thẳng lên mặt phẳng.
- Định nghĩa và công thức tính góc giữa đường thẳng và mặt phẳng thông qua hình chiếu.
- Ứng dụng vào các bài toán thực tế như dựng hình, tính góc, chứng minh vuông góc và tính khoảng cách.
Hãy cùng Dethitracnghiem.vn tìm hiểu về đề thi này và tham gia làm kiểm tra ngay lập tức!
Trắc nghiệm Toán 11: Bài 24 – Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng
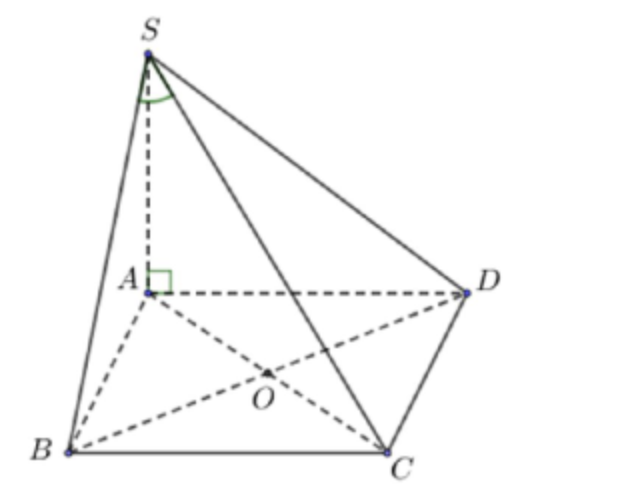
Câu 1: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA vuông góc vưới mp(ABCD) và \(SA = a\sqrt{6}\) (hình vẽ). Gọi \(\alpha\) là góc giữa đường thẳng SB và mp(SAC). Tính \(sin\alpha\) ta được kết quả là
A. \(\dfrac{\sqrt{14}}{4}\)
B. \(\dfrac{\sqrt{2}}{2}\)
C. \(\dfrac{\sqrt{2}}{3}\)
D. \(\dfrac{1}{5}\)
Câu 2: Cho hình vuông ABCD có độ dài cạnh là 2 cm và tâm O, trên đường thẳng qua O vuông góc với (ABCD) lấy điểm S sao cho \(SO = \sqrt{2}\). Tính góc giữa SA và (ABCD)
A. \(30^\circ\)
B. \(45^\circ\)
C. \(60^\circ\)
D. \(90^\circ\)
Câu 3: Cho hình lăng trụ đều ABC.A’B’C’ có \(AB = \sqrt{3}\) và AA’ = 1. Góc tạo bởi đường thẳng AC’ và (ABC) bằng
A. \(30^\circ\)
B. \(45^\circ\)
C. \(60^\circ\)
D. \(75^\circ\)
Câu 4: Cho hình chóp S.ABCD đáy là hình vuông, SA vuông góc với đáy và SA = a. Góc giữa SB và đáy bằng \(45^\circ\). Tính diện tích đáy theo a
A. \(\dfrac{a^2}{2}\)
B. \(a^2\sqrt{2}\)
C. \(a^2\)
D. \(2a^2\)
Câu 5: Cho hình chóp S.ABCD đáy là hình chữ nhật, SA⊥(ABCD). Khi đó góc giữa SB và (SAD) là
A. \(\widehat{BSA}\)
B. \(\widehat{BSD}\)
C. \(\widehat{SBA}\)
D. \(\widehat{SBD}\)
Câu 6: Cho hình chóp S. ABC có SA ⊥ (ABC); tam giác ABC đều cạnh a và SA = a. Tìm góc giữa đường thẳng SC và mặt phẳng (ABC)
A. \(30^\circ\)
B. \(45^\circ\)
C. \(60^\circ\)
D. \(90^\circ\)
Câu 7: Cho hình hóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh AB = a , \(AD = \sqrt{3}a\). Cạnh bên \(SA = a\sqrt{2}\) và vuông góc mặt phẳng đáy. Góc giữa đường thẳng SB và mặt phẳng (SAC) bằng
A. \(30^\circ\)
B. \(45^\circ\)
C. \(60^\circ\)
D. \(75^\circ\)
Câu 8: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB = BC = a, \(BB’ = a\sqrt{3}\). Tính góc giữa đường thẳng A’B và mp(BCC’B’)
A. \(30^\circ\)
B. \(45^\circ\)
C. \(60^\circ\)
D. \(90^\circ\)
Câu 9: Cho hình chóp S.ABCD đáy là hình chữ nhật, SA⊥(ABCD). Khi đó góc giữa SC và (SAB) là
A. \(\widehat{CSA}\)
B. \(\widehat{CSB}\)
C. \(\widehat{SCA}\)
D. \(\widehat{SCB}\)
Câu 10: Trong các khẳng định sau, khẳng định nào đúng
A. Góc giữa đường thẳng a và mp (P) bằng góc giữa a và mp (Q) thì (P) song song với (Q)
B. Góc giữa đường thẳng a và mp (P) bằng góc giữa đường thẳng b và mp(P) thì a // b
C. Hai đường thẳng a và b song song thì góc giữa a và mp(P) bằng góc giữa b và mp (P)
D. Góc \(\alpha\) là góc giữa đường thẳng và mặt phẳng thì \(0^\circ \le \alpha \le 180^\circ\)
Câu 11: Cho hình chóp S.ABC có đấy là tam giác vuông cân tại A, SA vuông góc với đáy và \(SA = \dfrac{1}{2}BC\). Tính góc giữa SA và (SBC)
A. \(30^\circ\)
B. \(45^\circ\)
C. \(60^\circ\)
D. \(90^\circ\)
Câu 12: Cho hình lăng trụ ABC.A’B’C’ đáy ABC là tam giác vuông và \(CA = CB = a\sqrt{2}\). Tam giác A’AB đều và nằm trong mặt phẳng vuông góc với đáy. Tính giá trị tan của góc giữa A’C và (A’B’C’)
A. \(\dfrac{1}{\sqrt{3}}\)
B. \(\sqrt{3}\)
C. 0
D. 1
Câu 13: Cho hình chóp S. ABC có cạnh SA vuông góc với đáy. Góc giữa đường thẳng SB và mặt phẳng đáy là góc giữa hai đường thẳng nào dưới đây?
A. SB và AB
B. SB và SC
C. SA và SB
D. SB và BC
Câu 14: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, góc giữa SC và đáy bằng \(45^\circ\). Tính góc giữa SC và (SAD)
A. \(60^\circ\)
B. \(53^\circ\)
C. \(30^\circ\)
D. \(28^\circ\)
Câu 15: Cho hình chóp S. ABCD đáy là hình thoi tâm O, SO ⊥ (ABCD). Khi đó góc giữa SA và (SBD) là
A. \(\widehat{SAB}\)
B. \(\widehat{ASB}\)
C. \(\widehat{ASO}\)
D. \(\widehat{SCB}\)
Câu 16: Cho tứ diện ABCD có AB, BC và BD đôi một vuông góc với nhau. Trong các khẳng định sau khẳng định nào sai
A. Góc giữa AC và (ABD) là góc \(\widehat{CAB}\)
B. Góc giữa AC và (BCD) là góc \(\widehat{ACB}\)
C. Góc giữa AD và (ABC) là góc \(\widehat{ADB}\)
D. Góc giữa CD và (ABD) là góc \(\widehat{CDB}\)
Câu 17: Cho hình chóp tứ giác đều S. ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA, \(\alpha\) là góc tạo bởi đường thẳng EM và mp(SBD). Giá trị của tan\(\alpha\) bằng
A. 2
B. \(\sqrt{3}\)
C. 1
D. \(\sqrt{2}\)
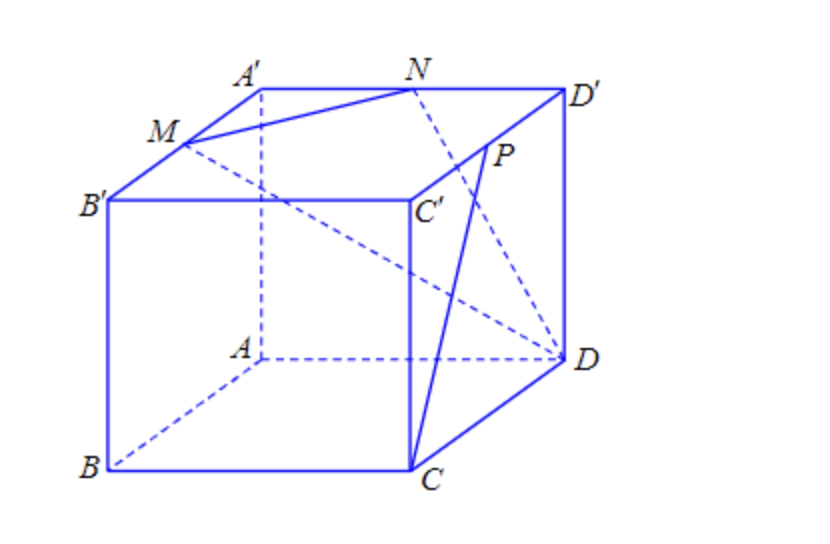
Câu 18: Cho hình hộp ABCD.A’B’C’D’ có M, N, P lần lượt là trung điểm của các cạnh A’B’, A’D’, C’D’. Góc giữa đường thẳng CP và mp(DMN) bằng?
A. \(30^\circ\)
B. \(45^\circ\)
C. \(60^\circ\)
D. \(0^\circ\)
Câu 19: Cho hình chóp S. ABCD đáy là hình thoi tâm O, SA ⊥ (ABCD). Khi đó góc giữa SD và (SAC) là
A. \(\widehat{SDA}\)
B. \(\widehat{DSA}\)
C. \(\widehat{SDO}\)
D. \(\widehat{DSO}\)
Câu 20: Cho tứ diện đều ABCD. Gọi \(\varphi\) là góc giữa đường thẳng AB và mặt phẳng (BCD). Tính \(cos\varphi\)
A. \(cos\varphi = 0\)
B. \(cos\varphi = \dfrac{1}{2}\)
C. \(cos\varphi = \dfrac{\sqrt{3}}{3}\)
D. \(cos\varphi = \dfrac{\sqrt{3}}{2}\)
Thảo Linh là một tác giả và biên tập viên giàu kinh nghiệm tại DeThiTracNghiem.vn, chuyên cung cấp các bộ đề thi thử trắc nghiệm chất lượng cao, giúp học sinh và sinh viên ôn tập hiệu quả. Với sự am hiểu sâu rộng về giáo dục và kỹ năng biên soạn nội dung học thuật, Thảo Linh đã đóng góp nhiều bài viết giá trị, giúp người học tiếp cận kiến thức một cách hệ thống và dễ hiểu.
