Trắc nghiệm Toán 11: Bài 25 – Hai mặt phẳng vuông góc là một trong những đề thi thuộc chương VII – Quan hệ vuông góc trong không gian trong chương trình Toán 11, với trọng tâm xoay quanh mối quan hệ vuông góc giữa hai mặt phẳng trong không gian ba chiều.
Trong bài học này, học sinh sẽ cần nắm vững điều kiện để hai mặt phẳng vuông góc, cách sử dụng vectơ pháp tuyến của các mặt phẳng để xác định mối quan hệ vuông góc giữa chúng. Đây là một kiến thức quan trọng trong hình học không gian, giúp giải quyết các bài toán liên quan đến góc giữa hai mặt phẳng, tính toán khoảng cách giữa các mặt phẳng, và các ứng dụng trong dựng hình. Các trọng tâm chính cần lưu ý bao gồm:
- Điều kiện và cách xác định khi hai mặt phẳng vuông góc với nhau.
- Sử dụng vectơ pháp tuyến của các mặt phẳng để kiểm tra và chứng minh mối quan hệ vuông góc.
- Ứng dụng trong các bài toán tính góc và khoảng cách giữa các mặt phẳng trong không gian.
Hãy cùng Dethitracnghiem.vn tìm hiểu về đề thi này và tham gia làm kiểm tra ngay lập tức!
Trắc nghiệm Toán 11: Bài 25 – Hai mặt phẳng vuông góc
Câu 1: Trong không gian cho tam giác đều SAB và hình vuông ABCD cạnh a nằm trên hai mặt phẳng vuông góc. Góc \(\varphi\) là góc giữa hai mặt phẳng (SAB) và (SCD). Mệnh đề nào sau đây đúng
A. \(tan\varphi = \sqrt{3}\)
B. \(tan\varphi = \dfrac{2\sqrt{3}}{3}\)
C. \(tan\varphi = \sqrt{2}\)
D. \(tan\varphi = 2\sqrt{3}\)
Câu 2: Cho hình chóp tứ giác đều có cạnh đáy bằng \(a\sqrt{2}\) và chiều cao bằng \(\dfrac{a\sqrt{2}}{2}\). Tan của góc giữa mặt bên và mặt đáy bằng:
A. 1
B. \(\dfrac{1}{\sqrt{3}}\)
C. \(\dfrac{3}{4}\)
D. \(\sqrt{3}\)
Câu 3: Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng nhau. Gọi \(\alpha\) là góc giữa hai mặt phẳng (AB’C’) và (A’BC), tính cos\(\alpha\)
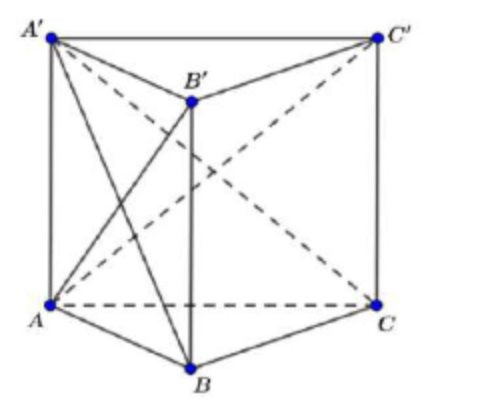
A. \(\dfrac{1}{7}\)
B. \(\dfrac{4}{7}\)
C. \(\dfrac{2\sqrt{1}}{7}\)
D. \(\dfrac{\sqrt{7}}{7}\)
Câu 4: Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = 4a, AD = 3a. Các cạnh bên đều có độ dài 5a. Tính góc \(\alpha\) giữa mp(SBC) và (ABCD)
A. \(\alpha \approx 75^\circ 46’\)
B. \(\alpha \approx 71^\circ 21’\)
C. \(\alpha \approx 68^\circ 31’\)
D. \(\alpha \approx 65^\circ 21’\)
Câu 5: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có bốn mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
B. Nếu hình hộp có ba mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
C. Nếu hình hộp có hai mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
D. Nếu hình hộp có năm mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và SA = SC, SB = SD. Mệnh đề nào sau đây sai?
A. \(SC \perp (SBD)\)
B. \(SO \perp (ABCD)\)
C. \((SBD) \perp (ABCD)\)
D. \((SAC) \perp (ABCD)\)
Câu 7: Cho hình lăng trụ tứ giác đều ABCD.A”B’C’D’. Mặt phẳng (AB’C) vuông góc với mặt phẳng nào sau đây?
A. (D’BC)
B. (B’BD)
C. (D’AB)
D. (BA’C’)
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt đáy. Góc giữa hia mặt phẳng (SCD) và (ABCD) bằng
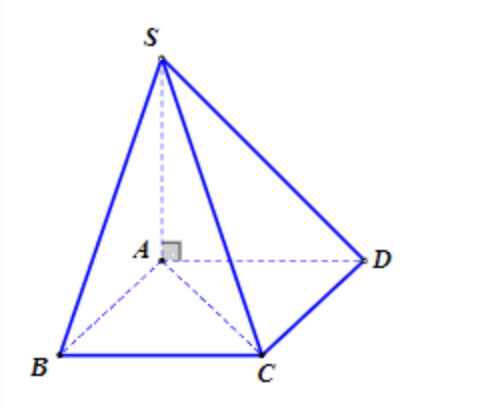
A. \(\widehat{SDA}\)
B. \(\widehat{SCA}\)
C. \(\widehat{SCB}\)
D. \(\widehat{ASD}\)
Câu 9: Cho hình chóp S.ABCD có đáy là tam giác ABC vuông tại B và cạnh bên SA vuông góc với mặt phẳng (ABC). Mệnh đề nào sau đây sai?
A. \(SA \perp BC\)
B. \(AB \perp BC\)
C. \(AB \perp SC\)
D. \(SB \perp BC\)
Câu 10: Khẳng định nào sau đây đúng?
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau
B. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau
C. Hai mặt phẳng song song khi và chỉ khi góc giữa chúng bằng \(0^\circ\).
D. Hai đường thẳng trong không gian cắt nhau khi và chỉ khi góc giữa chúng lớn hơn \(0^\circ\) và nhỏ hơn \(90^\circ\)
Câu 11: Cho hình chóp S.ABCD có đáy ABCD là hình thoi và SB vuông góc với mặt phẳng (ABCD). Mặt phẳng nào sau đây vuông góc với mặt phẳng (SBD)
A. (SBC)
B. (SAD)
C. (SCD)
D. (SAC)
Câu 12: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, cạnh bên SA vuông góc với (ABC). Gọi I là trung điểm cạnh AC, H là hình chiếu của I trên SC. Khẳng định nào sau đây đúng?
A. \((SBC) \perp (IHB)\)
B. \((SAC) \perp (SAB)\)
C. \((SAC) \perp (SBC)\)
D. \((SBC) \perp (SAB)\)
Câu 13: Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai mặt phẳng (A’B’CD) và (ABC’D’) bằng
A. \(45^\circ\)
B. \(60^\circ\)
C. \(30^\circ\)
D. \(90^\circ\)
Câu 14: Cho hình lập phương ABCD.A’B’C’D’. Tính góc giữa mp(ABCD) và (ACC’A’)
A. \(45^\circ\)
B. \(60^\circ\)
C. \(30^\circ\)
D. \(90^\circ\)
Câu 15: Chọn mệnh đề đúng trong các mệnh đề sau:
A. Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng tùy ý nằm trong mỗi mặt phẳng
B. Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó
C. Góc giữa hai mặt phẳng luôn là góc nhọn
D. Góc giữa hai mặt phẳng bằng góc giữa hai vecto chỉ phương của hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Câu 16: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác ABC vuông cân tại a. Gọi M là trung điểm của BC, mệnh đề nào sau đây sai?
A. \((ABB’) \perp (ACC’)\)
B. \((AC’M) \perp (ABC)\)
C. \((AMC’) \perp (BCC’)\)
D. \((ABC) \perp (ABA’)\)
Câu 17: Cho hình lập phương ABCD.A’B’C’D’. Tính góc giữa mp(A’BC) và (A’CD)
A. \(45^\circ\)
B. \(60^\circ\)
C. \(120^\circ\)
D. \(90^\circ\)
Câu 18: Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCd là hình thoi, \(AC = 2AA’ = 2a\sqrt{3}\). Góc giữa hai mặt phẳng (A’BD) và (C’BD) bằng
A. \(45^\circ\)
B. \(60^\circ\)
C. \(30^\circ\)
D. \(90^\circ\)
Câu 19: Trong các mệnh đề dưới đây mệnh đề nào sai?
A. Hình chóp tứ giác đều có tất cả các cạnh bằng nhau
B. Hình chóp tứ giác đều có các cạnh bên bằng nhau
C. Hình chóp tứ giác đều có đáy là hình vuông
D. Hình chóp tứ giác đều có hình chiếu vuông góc của đỉnh lên đáy trùng với tâm của đáy
Câu 20: Cho hình chóp S.ABC là tam giác cân tại B, cạnh bên SA vuông góc với đáy, I là trung điểm AC, H là hình chiếu của I lên SC. Khẳng định nào sau đây đúng?
A. \((BIH) \perp (SBC)\)
B. \((SAC) \perp (SAB)\)
C. \((SBC) \perp (ABC)\)
D. \((SAC) \perp (ABC)\)
Thảo Linh là một tác giả và biên tập viên giàu kinh nghiệm tại DeThiTracNghiem.vn, chuyên cung cấp các bộ đề thi thử trắc nghiệm chất lượng cao, giúp học sinh và sinh viên ôn tập hiệu quả. Với sự am hiểu sâu rộng về giáo dục và kỹ năng biên soạn nội dung học thuật, Thảo Linh đã đóng góp nhiều bài viết giá trị, giúp người học tiếp cận kiến thức một cách hệ thống và dễ hiểu.
