Trắc nghiệm Toán 11 Bài 10 – Đường thẳng và mặt phẳng trong không gian thuộc Chương IV: Quan hệ song song trong không gian trong chương trình Toán 11. Đây là chương mở đầu cho phần hình học không gian, giúp học sinh hình dung và mô tả các mối quan hệ giữa các đối tượng hình học trong không gian ba chiều một cách trực quan và chính xác.
Trắc nghiệm Toán 11: Bài 10 – Đường thẳng và mặt phẳng trong không gian là một trong những đề thi thuộc Chương IV – Quan hệ song song trong không gian trong chương trình Toán 11. Trong đề thi này, học sinh cần nắm vững các kiến thức cơ bản như: khái niệm điểm, đường thẳng, mặt phẳng trong không gian; các mối quan hệ giữa chúng như song song, cắt nhau, hoặc trùng nhau; và cách biểu diễn hình học của các đối tượng đó qua hình vẽ. Ngoài ra, học sinh cũng cần biết cách xác định giao điểm, giao tuyến và phân biệt các vị trí tương đối của đường và mặt trong không gian.
Hãy cùng Dethitracnghiem.vn tìm hiểu về đề thi này và tham gia làm kiểm tra ngay lập tức!
Trắc nghiệm Toán 11 Bài 10 – Đường thẳng và mặt phẳng trong không gian
Câu 1: Trong phát biểu sau đây, phát biểu nào đúng?
A. Hình chóp có tất cả các mặt là hình tam giác
B. Tất cả các mặt bên của hình chóp là hình tam giác
C. Tồn tại một mặt bên của hình chóp không phải là hình tam giác
D. Số cạnh bên của hình chóp bằng số mặt của nó
Câu 2: Một mặt phẳng hoàn toàn được xác định nếu biếu điều nào sau đây?
A. Ba điểm mà nó đi qua
B. Một điểm và một đường thẳng thuộc nó
C. Ba điểm không thẳng hàng
D. Hai đường thẳng thuộc mặt phẳng
Câu 3: Trong các phát biều sau, phát biểu nào đúng?
A. Nếu hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
B. Hai mặt phẳng có thể có đúng hai điểm chung
C. Nếu hai mặt phẳng có một điểm chung thì chúng có chung một đường thẳng duy nhất hoặc mọi điểm thuộc mặt phẳng này đều thuộc mặt phẳng kia.
D. Hai mặt phẳng luôn có điểm chung.
Câu 4: Cho hình tứ diện ABCD, phát biểu nào sau đây là đúng?
A. AC và BD cắt nhau
B. AC và BD không có điểm chung
C. Tồn tại một mặt phẳng chứa AD và BC
D. AB và CD song song với nhau
Câu 5: Cho hình chóp S.ABCD, O là giao điểm của AC và BD, phát biểu nào sau đây là đúng?
A. Giao tuyến của (SAC) và (SBD) là SO.
B. Giao tuyến của (SAB) và (SCD) là điểm S.
C. Giao tuyến của (SBC) và (SCD) là SK, với K là giao điểm của SD và BC.
D. Giao tuyến của (SOC) và (SAD) là SM, với M là giao điểm của AC và SD.
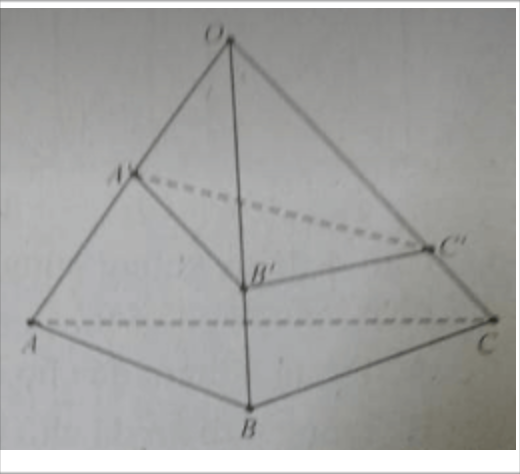
Câu 7: Cho hình chóp O.ABC, A’ là trung điểm của OA; các điểm B’, C’ tương ứng thuộc các cạnh OB, OC và không phải là trung điểm của các cạnh này. Phát biểu nào sau đây là đúng?
A. Giao tuyến của (OBC) và (A’B’C’) là A’B’;
B. Giao tuyến của (ABC) và (OC’A’) là CK, với K là giao điểm của C’B’ với CB
C. (ABC) và (A’B’C’) không cắt nhau
D. Giao tuyến của (ABC) và (A’B’C’) là MN, với M là giao điểm của AC và A’C’, N là giao điểm của BC và B’C’.
Câu 7: Trong các phát biểu sau, phát biểu nào đúng?
A. Hình tứ diện có 4 cạnh
B. Hình tứ diện có 4 mặt
C. Hình tứ diện có 6 đỉnh
D. Hình tứ diện có 6 mặt
Câu 8: Số cạnh của hình chóp tam giác là:
A. 5
B. 4
C. 6
D. 3
Câu 9: Hình biểu diễn nào sau đây vẽ đúng hình chóp?
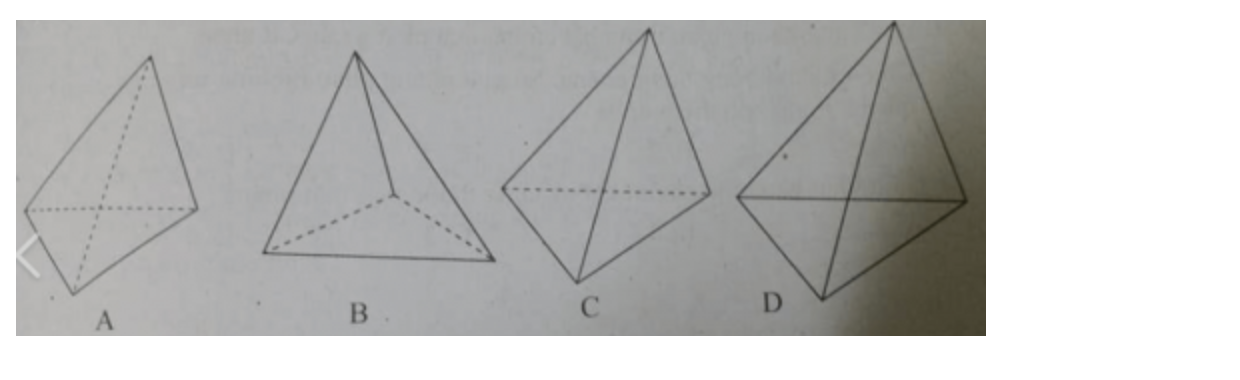
A. Hình a
B. Hình b
C. Hình c
D. Hình d
Câu 10: Hình biểu diễn nào sau đây vẽ đúng hình hộp?
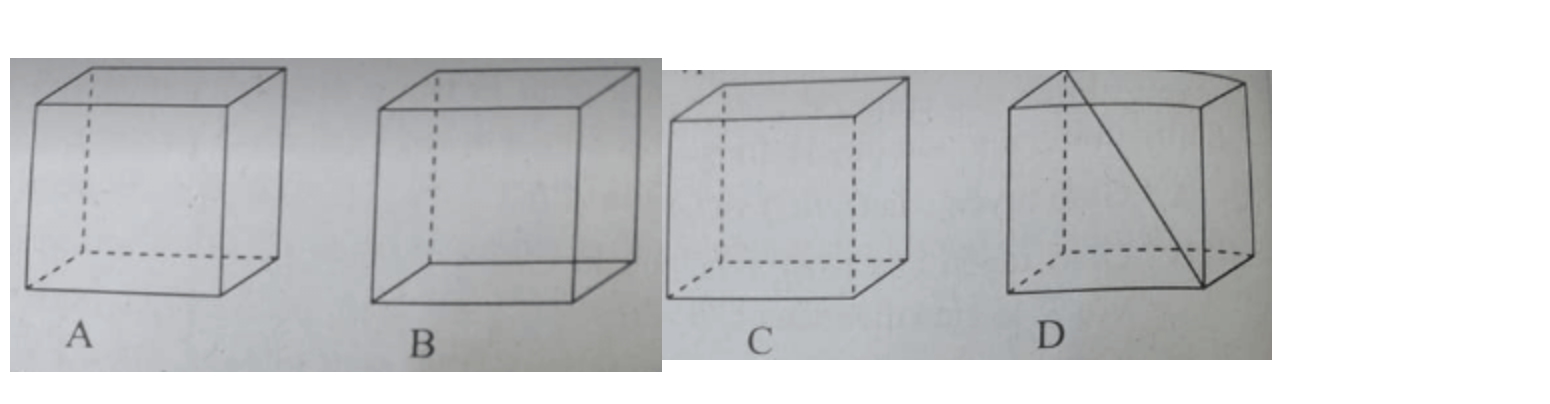
A. Hình a
B. Hình b
C. Hình c
D. Hình d
Câu 11: Cho 4 điểm không cùng thuộc một mặt phẳng. Trong các phát biểu sau đây, phát biểu nào là sai?
A. Trong 4 điểm đã cho không có ba điểm nào thẳng hàng
B. Trong 4 điểm đã cho luôn luôn tồn tại 3 điểm thuộc cùng 1 mặt phẳng
C. Số mặt phẳng đi qua 3 trong 4 điểm đã cho là 4
D. Số đoạn thẳng nối hai điểm trong 4 điểm đã cho là 6.
Câu 12: Có duy nhất một mặt phẳng đi qua
A. Hai đường thẳng
B. Một điểm và một đường thẳng
C. Ba điểm
D. Hai đường thẳng cắt nhau
Câu 13: Có một và chỉ một mặt phẳng đi qua
A. Ba điểm
B. Một điểm và một đường thẳng không chứa điểm đó.
C. Hai điểm
D. Bốn điển
Câu 14: Hai đường thẳng chéo nhau nếu.
A. Chúng không có điểm chung
B. Chúng không cắt nhau và không song song với nhau
C. Chúng không cùng nằm trong bất kì một mặt phẳng nào
D. Chúng không nằm trong bất cứ hai mặt phẳng nào cắt nhau.
Câu 15: Cho 4 điểm không đồng phẳng. Số mặt phẳng phân biệt mà mỗi mặt phẳng đi qua ba trong bốn điểm đó là:
A. 1
B. 2
C. 3
D. 4
Câu 16: Trong các khẳng định sau; khẳng định nào đúng?
A. Qua hai điểm phân biệt có duy nhất một mặt phẳng.
B. Qua ba điểm phân biệt bất kì có duy nhất một mặt phẳng.
C. Qua ba điểm không thẳng hàng có duy nhất một mặt phẳng.
D. Qua bốn điểm bất kì có duy nhất một mặt phẳng.
Câu 17: Trong không gian; cho 5 điểm không đồng phẳng. Có thể xác định được tối đa bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
A. 7
B. 8
C. 10
D. 6
Câu 18: Cho 5 điểm phân biệt: A; B; C; D; E trong đó không có 4 điểm nào đồng phẳng. Hỏi có bao nhiêu mặt phẳng tạo bởi 3 trong 5 điểm đã cho?
A. 8
B. 9
C. 10
D. 12
Câu 19: Cách xác định một mặt phẳng duy nhất là:
A. Ba điểm phân biệt.
B. Một điểm và một đường thẳng.
C. Hai đường thẳng cắt nhau.
D. Bốn điểm bất kì.
Câu 20: Cho hình vuông ABCD. Có thể xác định được bao nhiêu mặt phẳng chứa tất cả các đỉnh của hình vuông ABCD?
A. 1
B. 2
C. 3
D. 4
Thảo Linh là một tác giả và biên tập viên giàu kinh nghiệm tại DeThiTracNghiem.vn, chuyên cung cấp các bộ đề thi thử trắc nghiệm chất lượng cao, giúp học sinh và sinh viên ôn tập hiệu quả. Với sự am hiểu sâu rộng về giáo dục và kỹ năng biên soạn nội dung học thuật, Thảo Linh đã đóng góp nhiều bài viết giá trị, giúp người học tiếp cận kiến thức một cách hệ thống và dễ hiểu.
